【题目】小明同学将一张圆桌紧靠在矩形屋子的一角,与相邻两面墙相切,她把切点记为A、B,然后,她又在桌子边缘上任取一点P(异于A、B),则∠APB的度数为( )
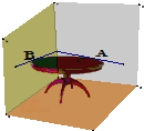
A. 45° B. 135° C. 45°或135° D. 90°或135°
参考答案:
【答案】C
【解析】试题分析:连接OA、OB,则∠MAO=∠MBO=90°即可求得弧AB所对的圆心角的度数,然后分P在优弧和劣弧上两种情况进行讨论,利用圆周角定理即可求解.
解:连接OA、OB,则∠MAO=∠MBO=90°,
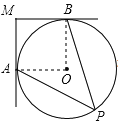
又∵∠M=90°,
∴四边形AOBM是矩形。
∴∠AOB=90°,
当P在AB所对的优弧上时,∠P=![]() ∠AOB=45°,
∠AOB=45°,
则当P在劣弧上时,∠P=180°45°=135°.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的
 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)甲
乙
进价(元/件)
22
30
售价(元/件)
29
40
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,D、E是BC边上的点,连接AD、AE,以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形△AD′E,连接D′C,若BD=CD′.
(1)求证:△ABD≌△ACD′;
(2)如图2,若∠BAC=120°,探索BD,DE,CE之间满足怎样的数量关系时,△CD′E是正三角形;
(3)如图3,若∠BAC=90°,求证:DE2=BD2+EC2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
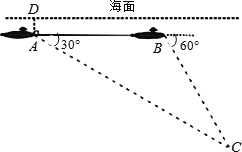
A. 2000米 B. 4000米 C. 2000米 D. (2000
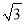 +500)米
+500)米 -
科目: 来源: 题型:
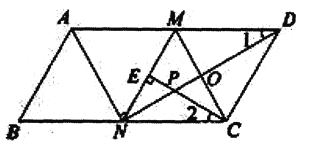
查看答案和解析>>【题目】如图,在
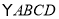 中,
中,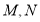 分别是
分别是 的中点,
的中点,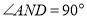 ,连接
,连接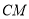 交
交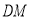 于点
于点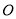 .
.
(1)求证:
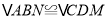 ;
;(2)过点
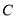 作
作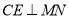 于点
于点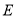 ,交
,交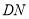 于点
于点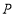 ,若
,若 ,求
,求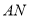 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形
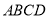 中,
中,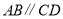 ,再添加下列其中一个条件后,四边形
,再添加下列其中一个条件后,四边形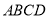 不一定是平行四边形的是( )
不一定是平行四边形的是( )A.
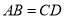 B.
B.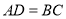 C.
C.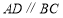 D.
D.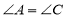
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 和
和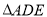 都是等边三角形,
都是等边三角形,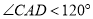 ,点
,点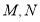 分别是
分别是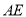 ,
, 的中点,连结
的中点,连结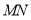 ,
,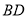 ,当
,当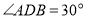 ,
,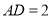 ,
,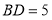 时,
时,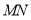 的长度为__________.
的长度为__________.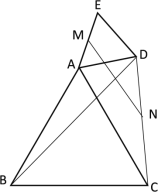
相关试题

