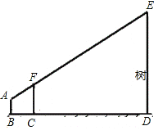
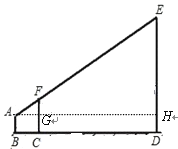
【题目】为了测量校园水平地面上一棵树的高度,数学兴趣小组利用一根标杆、皮尺,设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上,此同学眼睛距地面1.6米,标杆高为3.2米,且BC=2米,CD=6米,求树ED的高.
参考答案:
【答案】8米
【解析】
试题分析:过A作AH垂直ED,垂足为H,交线段FC与G,根据题意得出 △AFG∽△AEH,从而求出EH的长度,根据ED=EH+HD得出答案.
试题解析:如图,过A作AH垂直ED,垂足为H,交线段FC与G,
由题知,FG//EH, △AFG∽△AEH,![]()
又因为AG=BC=2,AH=BD=2+6=8,FG=FC-GC=3.2 -1.6=1.6, 所以![]() ,EH=6.4,
,EH=6.4,
∴ED=EH+HD=6.4+1.6=8 树ED的高为8米
-
科目: 来源: 题型:
查看答案和解析>>【题目】小敏为了解本市的空气质量情况,从环境监测网随机抽取了若干天的空气质量情况作为样本进行统计,绘制了如图所示的条形统计图和扇形统计图(部分信息未给出).
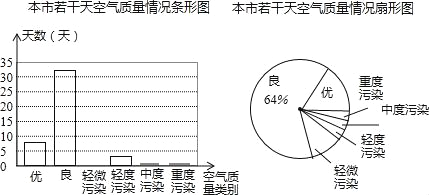
根据以上信息,如下结论错误的是( )
A.被抽取的天数为50天
B.空气轻微污染的所占比例为10%
C.扇形统计图中表示优的扇形的圆心角度数57.6°
D.估计该市这一年达到优和良的总天数不多于290天
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
-
科目: 来源: 题型:
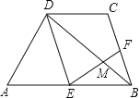
查看答案和解析>>【题目】 如图,梯形ABCD中,AB//CD,且AB=2CD,E,F分别是AB,BC的中点.
EF与BD相交于点M.
(1)求证:△EDM∽△FBM;
(2)若DB=9,求BM.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形边长分别为a、b、2,且a,b是关于x的一元二次方程
 的两根,求n的值.
的两根,求n的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校园商店经销甲、乙两种文具. 现有如下信息:

请根据以上信息,解答下列问题:
(1)甲、乙两种文具的零售单价分别为 元和 元.(直接写出答案)
(2)该校园商店平均每天卖出甲文具50件和乙文具120件.经调查发现,甲种文具零售单价每降0.1元,甲种文具每天可多销售10件.为了降价促销,使学生得到实惠,商店决定把甲种文具的零售单价下降m(m>0)元.在不考虑其他因素的条件下,当m定为多少时,可以使商店每天销售甲、乙两种文具获取的利润保持不变?
-
科目: 来源: 题型:
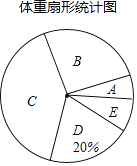
查看答案和解析>>【题目】某校为了解九年级学生的体重情况,随机抽取了九年级部分学生进行调查,将抽取学生的体重情况绘制如下不完整的统计图表,如图表所示,请根据图表信息回答下列问题:
体重频数分布表
组边
体重(千克)
人数
A
45≤x<50
12
B
50≤x<55
m
C
55≤x<60
80
D
60≤x<65
40
E
65≤x<70
16
(1)填空:①m=__(直接写出结果);
②在扇形统计图中,C组所在扇形的圆心角的度数等于__度;
(2)如果该校九年级有1000名学生,请估算九年级体重低于60千克的学生大约有多少人?
相关试题

