【题目】如图,抛物线y= ![]() x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣
x2+bx+c与x轴交于A、B两点,其中点B(2,0),交y轴于点C(0,﹣ ![]() ).直线y=mx+
).直线y=mx+ ![]() 过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.
过点B与y轴交于点N,与抛物线的另一个交点是D,点P是直线BD下方的抛物线上一动点(不与点B、D重合),过点P作y轴的平行线,交直线BD于点E,过点D作DM⊥y轴于点M.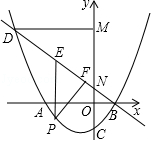
(1)求抛物线y= ![]() x2+bx+c的表达式及点D的坐标;
x2+bx+c的表达式及点D的坐标;
(2)若四边形PEMN是平行四边形?请求出点P的坐标;
(3)过点P作PF⊥BD于点F,设△PEF的周长为C,点P的横坐标为a,求C与a的函数关系式,并求出C的最大值.
参考答案:
【答案】
(1)
解:将B,C点坐标代入函数解析式,得 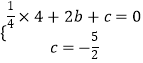 ,
,
解得 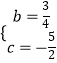 ,
,
抛物线的解析式为y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() .
.
∵直线y=mx+ ![]() 过点B(2,0),
过点B(2,0),
∴2m+ ![]() =0,
=0,
解得m=﹣ ![]() ,
,
直线的解析式为y=﹣ ![]() x+
x+ ![]() .
.
联立直线与抛物线,得 
∴ ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() =﹣
=﹣ ![]() x+
x+ ![]() ,
,
解得x1=﹣8,x2=2(舍),
∴D(﹣8,7 ![]() )
)
(2)
解:∵DM⊥y轴,
∴M(0,7 ![]() ),N(0,
),N(0, ![]() )
)
∴MN=7 ![]() ﹣
﹣ ![]() =6.
=6.
设P的坐标为(x, ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() ),E的坐标则是(x,﹣
),E的坐标则是(x,﹣ ![]() x+
x+ ![]() )
)
PE=﹣ ![]() x+
x+ ![]() ﹣(
﹣( ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() )=﹣
)=﹣ ![]() x2﹣
x2﹣ ![]() x+4,
x+4,
∵PE∥y轴,要使四边形PEMN是平行四边形,必有PE=MN,
即﹣ ![]() x2﹣
x2﹣ ![]() x+4=6,解得x1=﹣2,x2=﹣4,
x+4=6,解得x1=﹣2,x2=﹣4,
当x=﹣2时,y=﹣3,即P(﹣2,﹣3),
当x=﹣4时,y=﹣ ![]() ,即P(﹣4,﹣
,即P(﹣4,﹣ ![]() ),
),
综上所述:点P的坐标是(﹣2,﹣3)和)(﹣4,﹣ ![]() )
)
(3)
解:在Rt△DMN中,DM=8,MN=6,
由勾股定理,得
DN= ![]() =10,
=10,
∴△DMN的周长是24.
∵PE∥y轴,
∴∠PEN=∠DNM,
又∵∠PFE=∠DMN=90°,
∴△PEF∽△DMN,
∴ ![]() =
= ![]() ,
,
由(2)知PE=﹣ ![]() a2﹣
a2﹣ ![]() a+4,
a+4,
∴ ![]() =
= ![]() ,
,
∴C=﹣ ![]() a2﹣
a2﹣ ![]() a+
a+ ![]() ,
,
C=﹣ ![]() (a+3)2+15,
(a+3)2+15,
C与a的函数关系式为C=﹣ ![]() a2﹣
a2﹣ ![]() a+
a+ ![]() ,
,
当x=﹣3时,C的最大值是15
【解析】(1)根据待定系数法,可得抛物线的解析式,直线的解析式,根据解方程组,可得D点坐标;(2)根据y轴上两点间的距离是较大的纵坐标减较小的纵坐标,可得MN,PE的长,根据平行四边形的判定,可得关于x的方程,根据解方程,可得P的横坐标,根据自变量与函数值的对应关系,可得答案;(3)根据勾股定理,可得DN的长,根据相似三角形的判定与性质,可得 ![]() =
= ![]() ,根据比例的基本性质,可得答案.
,根据比例的基本性质,可得答案.
【考点精析】掌握平行四边形的判定和相似三角形的判定与性质是解答本题的根本,需要知道两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,若两条平行线EF,MN与直线AB,CD相交,则图中共有同旁内角的对数为( )
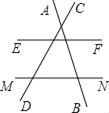
A. 4 B. 8 C. 12 D. 16
-
科目: 来源: 题型:
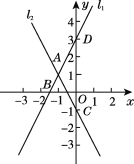
查看答案和解析>>【题目】已知直线l1:y1=2x+3与直线l2:y2=kx-1交于点A,点A的横坐标为-1,且直线l1与x轴交于点B,与y轴交于点D,直线l2与y轴交于点C.
(1)直线l2对应的函数表达式;
(2)连接BC,求S△ABC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了组织一个50人的旅游团开展“乡间民俗”游,旅游团住村民家,住宿客房有三人间、二人间、单人间三种,收费标准是三人间每人每晚20元,二人间每人每晚30元,单人间每人每晚50元,旅游团共住20间客房,旅游团如何安排住宿才能够使得住宿费最低,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,AB=8,BC=6,点O为对角线BD的中点,点P从点A出发,沿折线AD﹣DO以每秒1个单位长度的速度向终点O运动,当点P与点A不重合时,过点P作PQ⊥AB于点Q,以PQ为边向右作正方形PQMN,设正方形PQMN与△ABD重叠部分图形的面积为S(平方单位),点P运动的时间为t(秒).

(1)如图2,当点N落在BD上时,求t的值;
(2)当正方形PQMN的边经过点O时(包括正方形PQMN的顶点),求此时t的值;
(3)当点P在边AD上运动时,求S与t之间的函数关系式;
(4)写出在点P运动过程中,直线DN恰好平分△BCD面积时t的所有可能值. -
科目: 来源: 题型:
查看答案和解析>>【题目】看图填空:

(1)∠1和∠3是直线________被直线____所截得的______;
(2)∠1和∠4是直线_________被直线____所截得的______;
(3)∠B和∠2是直线_________被直线_____所截得的______;
(4)∠B和∠4是直线_________被直线_____所截得的_______
-
科目: 来源: 题型:
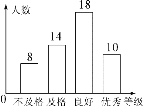
查看答案和解析>>【题目】我校进行“宪法知识”宣传培训后进行了一次测试.学生考分按标准划分为不合格、合格、良好、优秀四个等级,为了解全校的考试情况,对在校的学生随机抽样调查,得到如图所示的条形统计图,请结合统计图回答下列问题:
(1)该校抽样调查的学生人数为________人,抽样中考生分数的中位数所在等级是________;
(2)抽样中不及格的人数是多少?占被调查人数的百分比是多少?
相关试题

