【题目】某中学为了了解七年级学生体能状况,从七年级学生中随机抽取部分学生进行体能测试,测试结果分为A,B,C,D四个等级,并依据测试成绩绘制了如下两幅尚不完整的统计图:

(1)这次抽样调查的样本容量是 ,并补全条形统计图;
(2)在统计图中B等级所对应的圆心角为 ,D等级学生人数占被调查人数的百分比为 ;
(3)该校七年级学生有1600人,请你估计其中A等级的学生人数.
参考答案:
【答案】(1)50;补图见解析;(2)144°,8%;(3)该校七年级学生有1600人,估计其中A等级的学生人数约为512人.
【解析】
(1)由C等级的人数和其所占的百分比即可求出抽样调查的样本容量;求出B等级的人数即可补全条形图;
(2)用B等级的人数除以总人数得到其占被调查人数的百分比,乘以360°得到B等级所对应的圆心角度数;用D等级学生人数除以被调查人数,求出百分比;
(3)先求出A等级所占的百分比,进而可求出七年级学生其中A等级的学生人数.
(1)由条形统计图和扇形统计图可知总人数=10÷20%=50人,
所以B等级的人数=50﹣16﹣10﹣4=20人,
故答案为:50;
补全条形图如图所示:

(2)在统计图中B等级所对应的圆心角为![]() ,
,
D等级学生人数占被调查人数的百分比为![]() ,
,
故答案为:144°,8%;
(3)![]() (人),
(人),
该校七年级学生有1600人,估计其中A等级的学生人数约为512人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点D在反比例函数y=
 的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC=
的图象上,过点D作x轴的平行线交y轴于点B(0,3).过点A(5,0)的直线y=kx+b与y轴于点C,且BD=OC,tan∠OAC= 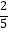 .
.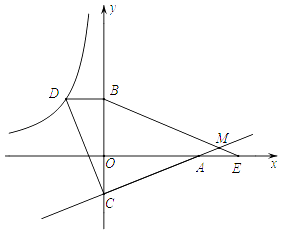
(1)求反比例函数y= 和直线y=kx+b的解析式;
和直线y=kx+b的解析式;
(2)连接CD,试判断线段AC与线段CD的关系,并说明理由;
(3)点E为x轴上点A右侧的一点,且AE=OC,连接BE交直线CA与点M,求∠BMC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D为BC边的任意一点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E、F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,D为BC的中点时,则线段DE与DF有何数量关系?请直接写出结论;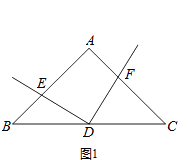
(2)如图2,若AB=kAC,D为BC的中点时,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请写出DE与DF的关系并说明理由;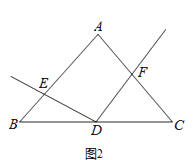
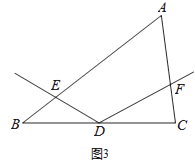
(3)如图3,若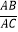 =a,且
=a,且 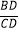 =b,直接写出
=b,直接写出 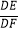 = .
= . 
-
科目: 来源: 题型:
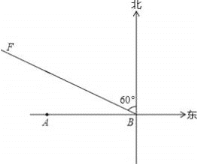
查看答案和解析>>【题目】如图,A市气象站测得台风中心在A市正东方向300千米的B处,以10
 千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.
千米/时的速度向北偏西60°的BF方向移动,距台风中心200千米范围内是受台风影响的区域.(1)A市是否会受到台风的影响?写出你的结论并给予说明;
(2)如果A市受这次台风影响,那么受台风影响的时间有多长?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为倡导绿色出行,平阳县在昆阳镇设立了公共自行车服务站点,小明对某站点公共自行车的租用情况进行了调查,将该站点一天中市民每次租用公共自行车的时间t(单位:分)(t≤120)分成A,B,C,D四个组进行各组人次统计,并绘制了如下的统计图,请根据图中信息解答下列问题:

(1)该站点一天中租用公共自行车的总人次为 , 表示A的扇形圆心角的度数是 .
(2)补全条形统计图.
(3)考虑到公共自行车项目是公益服务,公共自行车服务公司规定:市民每次使用公共自行收费2元,已知昆阳镇每天租用公共自行车(时间在2小时以内)的市民平均有5000人次,据此估计公共自行车服务公司每天可收入多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的图形中,所有四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形边长为7cm,设正方形A、B、C、D、E、F面积分别为SA、SB、SC、SD、SE、SF,则下列各式正确有()个.

① SA+SB+SC+SD=49;② SE+SF=49;③ SA+SB+SF=49;④ SC+SD+SE=4
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一张长方形纸片ABCD沿EF折叠后,ED与BC交点为G,D、C分别在M、N的位置上,若∠2-∠1=40°,则∠EFC的度数为( )
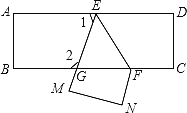
A. 115°B. 125°C. 135°D. 145°
相关试题

