Question

【题目】如图，把长方形纸片OABC放入直角坐标系中，使OA， OC分别落在x轴、y轴的正半轴上，连接AC，将翻折，点B落在该坐标平面内，设这个落点为D，CD交x轴于点E，已知CB=8，AB=4.

(1)求AC所在直线的函数关系式;

(2)求点E的坐标和的面积:

(3)求点D的坐标，并判断点(8， -4)是否在直线OD上，说明理由.

Answer 1

【答案】(1) y=;(2)10;(3) D坐标为（）,点（8，）在直线OD上，理由见解析；

【解析】

（1）根据已知求得A、C的坐标，然后根据待定系数法即可求解；（2）首先证明△ACE是等腰三角形，在直角△OCE中利用勾股定理即可求得OE的长，求得E的坐标，进而求得△ACE的面积；（3）作DF⊥x轴于点F，根据△ADE的面积求得D的纵坐标，然后在直角△ADF中，利用勾股定理求得AF的长，从而求得OF，即可得到D的坐标，然后利用待定系数法求得直线OD的解析式，然后把点（8，-4）代入判断即可；

解：（1） ∵OA，OC分别落在x轴、y轴的正半轴上，CB=8，AB=4．

∴A（8，0）、C（0，4），

设直线AC解析式为y=kx+b，

∴

解得：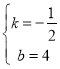

∴AC所在直线的函数关系式为y=；

（2）∵长方形OABC中，BC∥OA，

∴∠BCA=∠CAO，

又∵∠BCA=∠ACD，

∴∠ACD=∠CAO，

∴CE=AE；

设CE=AE=x，则OE=8-x，在直角△OCE中，OC2+OE2=CE2，

则，

解得：x=5；

则OE=8-5=3，

则E（3，0），

∴S△ACE=×5×4=10；

（3）如图，作DF⊥x轴于点F，

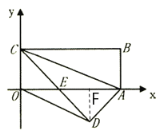
S△ACD=S△ABC=，

∴S△ADE=16-10=6，

又∵S△ADE= ，

∴×5×DF=6；

∴DF=，

在直角△ADF中，AF=，

则OF=8-；

∴D坐标为（）；

设直线OD的解析式为y=mx，则，

解得：m=，

则直线OD解析式为：y=x，

当x=8时，y=-4，则（8，）在直线OD上.