【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )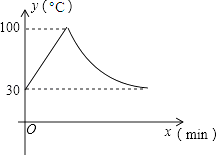
A.7:20
B.7:30
C.7:45
D.7:50
参考答案:
【答案】A
【解析】解:∵开机加热时每分钟上升10℃,
∴从30℃到100℃需要7分钟,
设一次函数关系式为:y=k1x+b,
将(0,30),(7,100)代入y=k1x+b得k1=10,b=30
∴y=10x+30(0≤x≤7),令y=50,解得x=2;
设反比例函数关系式为:y= ![]() ,
,
将(7,100)代入y= ![]() 得k=700,∴y=
得k=700,∴y= ![]() ,
,
将y=30代入y= ![]() ,解得x=
,解得x= ![]() ;
;
∴y= ![]() (7≤x≤
(7≤x≤ ![]() ),令y=50,解得x=14.
),令y=50,解得x=14.
所以,饮水机的一个循环周期为 ![]() 分钟.每一个循环周期内,在0≤x≤2及14≤x≤
分钟.每一个循环周期内,在0≤x≤2及14≤x≤ ![]() 时间段内,水温不超过50℃.
时间段内,水温不超过50℃.
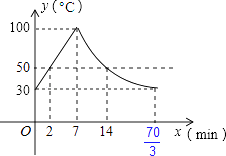
逐一分析如下:
选项A:7:20至8:45之间有85分钟.85﹣ ![]() ×3=15,位于14≤x≤
×3=15,位于14≤x≤ ![]() 时间段内,故可行;
时间段内,故可行;
选项B:7:30至8:45之间有75分钟.75﹣ ![]() ×3=5,不在0≤x≤2及14≤x≤
×3=5,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行;
时间段内,故不可行;
选项C:7:45至8:45之间有60分钟.60﹣ ![]() ×2=
×2= ![]() ≈13.3,不在0≤x≤2及14≤x≤
≈13.3,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行;
时间段内,故不可行;
选项D:7:50至8:45之间有55分钟.55﹣ ![]() ×2=
×2= ![]() ≈8.3,不在0≤x≤2及14≤x≤
≈8.3,不在0≤x≤2及14≤x≤ ![]() 时间段内,故不可行.
时间段内,故不可行.
综上所述,四个选项中,唯有7:20符合题意.
故答案为:A.
根据实际情况由开机加热时每分钟上升10℃,得到从30℃到100℃需要7分钟,设出一次函数关系式为y=k1x+b,将(0,30),(7,100)代入y=k1x+bk1=10,求出b=30,解得x=2;设反比例函数关系式为y= ![]() ,将(7,100)代
,将(7,100)代![]() 入得k=700,得到解析式
入得k=700,得到解析式![]() ,求出饮水机的一个循环周期为的时间,每一个循环周期内,分时间段分析,得出结论.
,求出饮水机的一个循环周期为的时间,每一个循环周期内,分时间段分析,得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若等腰三角形的周长为20 cm,底边长为x cm,一腰长为y cm,则y与x之间的函数表达式正确的是( )
A. y=20-2x(0<x<20) B. y=20-2x(0<x<10)
C. y=
 (20-x)(0<x<20) D. y=
(20-x)(0<x<20) D. y= (20-x)(0<x<10)
(20-x)(0<x<10) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.

(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )

A.122°
B.128°
C.132°
D.138° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点O是坐标原点,点A在y轴的正半轴上,坐标为
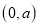 ,点B在x轴的负半轴上,坐标为
,点B在x轴的负半轴上,坐标为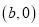 ,同时
,同时 满足
满足 ,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.
,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.
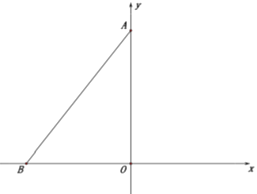
(1)求A、B两点坐标;
(2)若
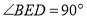 ,点D的横坐标为x,线段
,点D的横坐标为x,线段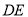 的长为d,请用含x的式子表示d;
的长为d,请用含x的式子表示d;(3)若
 ,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数. -
科目: 来源: 题型:
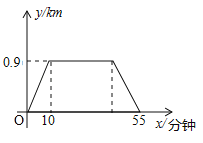
查看答案和解析>>【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.
-
科目: 来源: 题型:
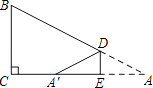
查看答案和解析>>【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
A.
B.3
C.2
D.1
相关试题

