【题目】如图,在平面直角坐标系中,点O是坐标原点,点A在y轴的正半轴上,坐标为![]() ,点B在x轴的负半轴上,坐标为
,点B在x轴的负半轴上,坐标为![]() ,同时
,同时![]() 满足
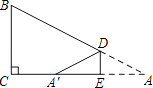
满足![]() ,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.
,连接AB,且AB=10.点D是x轴正半轴上的一个动点,点E是线段AB上的一个动点,连接DE.

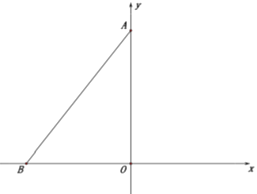
(1)求A、B两点坐标;
(2)若![]() ,点D的横坐标为x,线段
,点D的横坐标为x,线段![]() 的长为d,请用含x的式子表示d;
的长为d,请用含x的式子表示d;
(3)若![]() ,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
,AF、DF分别平分∠BAO、∠BDE,相交于点F,求∠F的度数.
参考答案:
【答案】(1)A(0,8),B(-6,0);(2)d=![]() (x>0);(3)∠AFD=85°.
(x>0);(3)∠AFD=85°.
【解析】
(1)解方程组求出a、b的值即可得答案;
(2)如图,连接AD,根据A、B坐标可得OA、OB的长,由点D坐标可求出BD的长,利用△ABD的面积即可得答案;
(3)如图,延长AF,交BD于点C,根据三角形内角和定理可得∠BAO-∠BDE=10°,根据三角形外角性质及角平分线的定义可得∠AFD=∠ACD+![]() ∠BDE,由直角三角形两直角互余的关系及角平分线的定义可得∠ACD=90°-
∠BDE,由直角三角形两直角互余的关系及角平分线的定义可得∠ACD=90°-![]() ∠BAO,进而可得∠AFD=90°-
∠BAO,进而可得∠AFD=90°-![]() (∠BAO-∠BED),即可得答案.
(∠BAO-∠BED),即可得答案.
(1)∵![]() 满足
满足![]() ,
,
∴解方程组得![]() ,
,
∴A点坐标为(0,8),B点坐标为(-6,0).
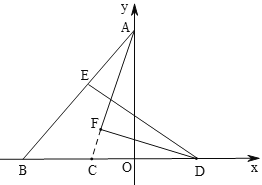
(2)如图,连接AD,
∵A(0,8),B(-6,0),
∴OA=8,OB=6,
∵点D是x轴正半轴上的一个动点,点D的横坐标为x,
∴OD=x,
∴BD=6+x,
∵AB=10,DE=d,∠BED=90°,
∴S△BAD=![]() AB·DE=
AB·DE=![]() BD·OA,即10d=8(6+x),
BD·OA,即10d=8(6+x),
∴d=![]() (x>0).
(x>0).

(3)如图,延长AF,交BD于C,
∵AF、DF分别平分∠BAO、∠BDE,
∴∠CAO=![]() ∠BAO,∠CDF=
∠BAO,∠CDF=![]() ∠BDE,
∠BDE,
∵∠BED=100°,∠BOA=90°,
∴∠B=180°-∠BED-∠BDE=80°-∠BDE,∠B=90°-∠BAO,
∴80°-∠BDE=90°-∠BAO,
∴∠BAO-∠BDE=10°,
∵∠ACD=90°-∠CAO=90°-![]() ∠BAO,
∠BAO,
∴∠AFD=∠ACD+∠CDF= 90°-![]() ∠BAO +
∠BAO +![]() ∠BDE=90°-
∠BDE=90°-![]() (∠BAO-∠BDE)=85°.
(∠BAO-∠BDE)=85°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx﹣4与x轴交于A(4,0)、B(﹣2,0)两点,与y轴交于点C,点P是线段AB上一动点(端点除外),过点P作PD∥AC,交BC于点D,连接CP.

(1)求该抛物线的解析式;
(2)当动点P运动到何处时,BP2=BDBC;
(3)当△PCD的面积最大时,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】AB为⊙O的直径,点C、D在⊙O上.若∠ABD=42°,则∠BCD的度数是( )

A.122°
B.128°
C.132°
D.138° -
科目: 来源: 题型:
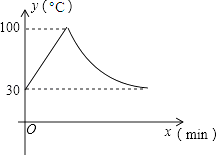
查看答案和解析>>【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A.7:20
B.7:30
C.7:45
D.7:50 -
科目: 来源: 题型:
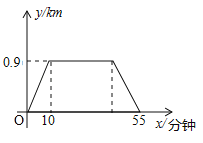
查看答案和解析>>【题目】小明从家到图书馆看报然后返回,他离家的距离y与离家的时间x之间的对应关系如图所示,如果小明在图书馆看报30分钟,那么他离家50分钟时离家的距离为 km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,∠C=90°,BC=3,D,E分别在AB、AC上,将△ADE沿DE翻折后,点A落在点A′处,若A′为CE的中点,则折痕DE的长为( )
A.
B.3
C.2
D.1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AE平分∠BAD交BC于点E,AE⊥DE,∠1+∠2=90°,M、N分别是BA,CD延长线上的点,∠EAM和∠EDN的平分线交于点F,下列结论:①AB∥CD;②∠AEB+∠ADC=180°;③DE平分∠ADC;④∠F为定值.其中结论正确的有( )

A. 4个B. 1个C. 2个D. 3个
相关试题

