Question

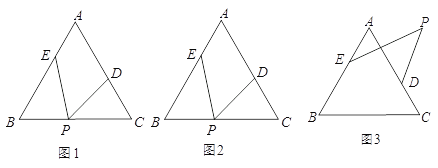
【题目】△ABC中，∠A=60°，点D、E分别是△ABC边AC、AB上的点(不与A、B、C重合)，点P是一动点，令∠PDC=∠1，∠PEB=∠2，∠DPE=∠α．

（1）若点P在边BC上，如图l，且∠α=50°，则∠1+∠2=　 　°．

（2）若点P在边BC上运动，如图2，试判断∠α、∠1、∠2之间的关系，并证明．

（3）直接写出：若点P运动到△ABC形外，如图3，则∠α、∠l、∠2之间的关系为 ．

Answer 1

【答案】（1）110°；（2）猜想：∠1+∠2=60°+∠ 证明见解析；（3）∠2－∠1+∠=60°

【解析】试题分析：（1）连接PA，根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PAD+∠APD，∠2=∠PAE+∠APE，再表示出∠1+∠2即可；（2）利用（1）中所求得出答案即可；（3）利用三角形内角和定理以及邻补角的性质可得出．

试题解析：

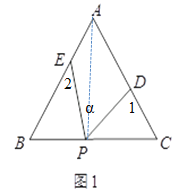
(1)如图，连接PC，

∵∠1=∠PAD+∠APD，∠2=∠PAE+∠APE，

∴∠1+∠2=∠PAD+∠APD+∠PAE+∠APE=∠DPE+∠A，

∵∠DPE=∠α=50°，∠A=60°，

∴∠1+∠2=50°+60°=110°

故答案为：110°；

(2)如图：连接PA，

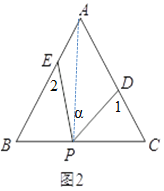
∵∠1=∠PAD+∠APD，∠2=∠PAE+∠APE

∴∠1+∠2=∠PAD+∠APD+∠PAE+∠APE=∠DPE+∠A，

∵∠A=60°，∠DPE=∠α，

∴∠1+∠2=60°+∠α；

故答案为：∠1+∠2=60°+∠α；

(3)如图，

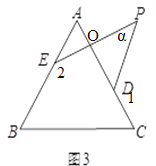
∵∠2=∠A+∠AOE，

∠1=∠α+∠POD；

∠AOE=∠POD

∴∠1∠2=∠A-∠α

即∠1∠2+∠α==60°