搜索
【题目】若∠AOB=70°,过点O作射线OC,∠AOC=30°，则∠COB=______.
参考答案：
【答案】40°或100°
【解析】当OC在∠AOB内部时，∠COB=∠AOB-∠AOC=70°-30°=40°；
当OC在∠AOB外时，∠COB=∠AOB+∠AOC=70°+30°=100°.
故答案为40°或100°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系XOY中，有A(3 , 2) ,B (－1 ,－4 )，P是X轴上的一点，Q是Y轴上的一点，若以点A,B,P,Q四个点为顶点的四边形是平行四边形，则Q点的坐标是______．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知关于x的一元二次方程（a+c）x2+2bx+（a﹣c）=0，其中a、b、c分别为△ABC三边的长．
（1）如果x=﹣1是方程的根，试判断△ABC的形状，并说明理由；
（2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
（3）如果△ABC是等边三角形，试求这个一元二次方程的根．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点A，B的坐标分别是（﹣3，0），（0，6），动点P从点O出发，沿x轴正方向以每秒1个单位的速度运动，同时动点C从点B出发，沿射线BO方向以每秒2个单位的速度运动．以CP，CO为邻边构造PCOD，在线段OP延长线上取点E，使PE=AO，设点P运动的时间为t秒．
（1）当点C运动到线段OB的中点时，求t的值及点E的坐标；
（2）当点C在线段OB上时，求证：四边形ADEC为平行四边形；
（3）在线段PE上取点F，使PF=2，过点F作MN⊥PE，截取FM=
，FN=1，且点M，N分别在第一、四象限，在运动过程中，当点M，N中，有一点落在四边形ADEC的边上时，直接写出所有满足条件的t的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】将抛物线y=x2﹣2x+1向下平移2个单位，再向左平移1个单位，所得抛物线的解析式是（ ）
A. y=x2﹣2x﹣1 B. y=x2+2x﹣1 C. y=x2﹣2 D. y=x2+2
-
科目： 来源： 题型：
查看答案和解析>>【题目】一组数据-1，3，7，4的极差是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，等边三角形ABD与等边三角形ACE具有公共顶点A，连接CD，BE，交于点P.
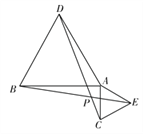
（1）观察度量，
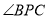的度数为＿＿＿＿.（直接写出结果）（2）若绕点A将△ACE旋转，使得
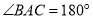，请你画出变化后的图形.（示意图）（3）在（2）的条件下，求出
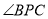的度数.
相关试题
