搜索
【题目】某段公路经测算发现，匀速行驶的车辆通过该段公路时，所需时间t（h）与行驶速度v（km/h）满足反比例函数关系，其图象为如图所示的一段曲线．且端点为A（40，1）和B（m，0.5）．
（1）求t与v的函数关系式及m的值；
（2）若该段公路限速50km/h，求通过该路段需要的最短时间和这段公路的长．
参考答案：
【答案】
（1）解：由题意，可设t与v的函数关系式为t= k v （k≠0），
∵函数t= 
经过点A（40，1），
∴1= 
，解得k=40，
∴t与v的函数关系式为t= 
；
把B（m，0.5）代入t= ，
得0.5= 
，解得m=80
（2）解：把v=50代入t= ，得t= 
=0.8，
则通过该路段需要的最短时间是0.8小时，这段公路的长为40km．
【解析】利用图像寻找一点坐标代入解析式即可；（2）将v=50代入反比例函数解析式即可.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知
中，
，
，点D为直线BC上的一动点
点D不与点B、C重合
，以AD为边作
，使
，
，连接CE．发现问题：
如图1，当点D在边BC上时，
请写出BD和CE之间的位置关系为______，并猜想BC和CE、CD之间的数量关系：______．尝试探究：
如图2，当点D在边BC的延长线上且其他条件不变时，中BD和CE之间的位置关系、BC和CE、CD之间的数量关系是否成立？若成立，请证明；若不成立，请写出新的数量关系，说明理由；拓展延伸：
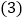如图3，当点D在边CB的延长线上且其他条件不变时，若
，
，求线段ED的长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：直线
，点E，F分别在直线AB，CD上，点M为两平行线内部一点．（1）如图1，∠AEM，∠M，∠CFM的数量关系为________；(直接写出答案)
（2）如图2，∠MEB和∠MFD的角平分线交于点N，若∠EMF等于130°，求∠ENF的度数；
（3）如图3，点G为直线CD上一点，延长GM交直线AB于点Q，点P为MG上一点，射线PF、EH相交于点H，满足
，
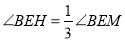，设∠EMF=α，求∠H的度数(用含α的代数式表示)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在2019年端午节前夕，某商场投入13800元资金购进甲、乙两种商品共500件，两种商品的成本价和销售价如下表所示：
商品 单价（元/件）
成本价
销售价
甲
24
36
乙
33
48
（1）该商场购进两种商品各多少件？
（2）这批商品全部销售完后，该商场共获利多少元？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，把边长为a的一块正方形纸板的四角，各剪去一个边长为b
的小正方形．
（1）求该纸板剩余部分（阴影部分）的面积；（用含a、b的代数式表示）
（2）当a=35cm，b=2.5cm时，请计算出剩余部分的面积；
（3）若将剩余的纸板按中间的虚线折成一个无盖的纸盒，求纸盒的容积；（用含a、b的代数式表示）
-
科目： 来源： 题型：
查看答案和解析>>【题目】探究：如何把多项式x2+8x+15因式分解？
（1）观察：上式能否可直接利用完全平方公式进行因式分解？ 答： ；
（阅读与理解）：由多项式乘法，我们知道(x+a)(x+b)=x2+(a+b)x+ab，将该式从右到左地使用，即可对形如x2+(a+b)x+ab的多项式进行因式分解，即：
x2+(a+b)x+ab=(x+a)(x+b)
此类多项式x2+(a+b)x+ab的特征是二次项系数为1，常数项为两数之积，一次项系数为这两数之和．
（2）猜想并填空： x2+8x+15= x2+[( ) +( )]x + ( )×( )=(x+ )(x+ )
（3）上面多项式x2+8x+15的因式分解是否正确，我们需要验证．请写出验证过程．
（4）请运用上述方法将下列多项式进行因式分解：
① x2+8x+12 ② x2-x-12
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，∠BAD＝130°，∠B＝∠D＝90°，点E，F分别是线段BC，DC上的动点．当△AEF的周长最小时，则∠EAF的度数为（ ）
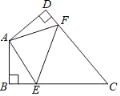
A. 90°B. 80°C. 70°D. 60°
相关试题
