【题目】在平面直角坐标系![]() 中,对于任意一点
中,对于任意一点![]() ,定义点
,定义点![]() 的“离心值”
的“离心值”![]() 为:
为: 时,例如对于点
时,例如对于点![]() ,因为
,因为![]() ,所以
,所以![]() .
.
解决下列问题:
(1)已知![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值,并将
的值,并将![]() ,
,![]() ,
,![]() 按从小到大的顺序排列(用“<”连接);
按从小到大的顺序排列(用“<”连接);
(2)如图,点![]() ,线段
,线段![]() 上的点
上的点![]() ,
,
①若![]() ,求点
,求点![]() 的坐标;
的坐标;
②在图中画出满足![]() 的点
的点![]() 组成的图形,并用语言描述该图形的特征;
组成的图形,并用语言描述该图形的特征;

参考答案:
【答案】(1)![]() ,
,![]() ;(2)①
;(2)①![]() ,
,![]() ;②见解析.
;②见解析.
【解析】
(1)根据“离心值”的定义求解即可;
(2)①由题意得,点P,点Q在直线x=-![]() 上,再根据“离心值”的定义求出y的值,即可确定P、Q的坐标;
上,再根据“离心值”的定义求出y的值,即可确定P、Q的坐标;
②根据“离心值”的定义,求出M的坐标,根据图形进行描述即可.
(1)∵|-![]() |>|-1|
|>|-1|
∴![]() =|-
=|-![]() |=
|=![]() ;
;
∵|0|<|5|,
∴![]() =5,
=5,
∵|-3|=3,
∴![]() =3,
=3,
∴![]()
(2)①∵点![]()
∴![]() ,且线段
,且线段![]() 轴
轴
对于线段![]() 上的点
上的点![]() ,它的横坐标
,它的横坐标![]() ,纵坐标
,纵坐标![]() 满足
满足![]()
∴线段![]() 上满足
上满足![]() 的点
的点![]() 的坐标为
的坐标为![]() ,
,![]() .
.
②根据离心值的定义可知,满足![]() 的点
的点![]() 组成的图形如图所示,
组成的图形如图所示,
该图形是线段![]() ,其中
,其中![]()

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边三角形网格中建立平面斜坐标系
 ,对于其中的“格点
,对于其中的“格点 ”(落在网格线交点处的点),过点
”(落在网格线交点处的点),过点 分别做
分别做 轴,
轴,  轴的平行线,找到平行线与另一坐标轴的交点的
轴的平行线,找到平行线与另一坐标轴的交点的 坐标和
坐标和 坐标,记这个有序数对
坐标,记这个有序数对 为它的坐标,如
为它的坐标,如 ,
, ,规定当点在
,规定当点在 轴上时,
轴上时, 坐标为0,如
坐标为0,如 ;当点在
;当点在 轴上时,
轴上时, 坐标为0.
坐标为0.(1)原点
 的坐标为 ,格点
的坐标为 ,格点 的坐标为 .
的坐标为 .(2)在图中画出点
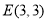 ,
,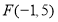 的位置;
的位置;(3)直线
 上的格点
上的格点 的坐标满足的条件是 (其中
的坐标满足的条件是 (其中 为整数).
为整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究逼近
 的有理近似值.
的有理近似值.方法介绍:
经过
 步操作(
步操作( 为正整数)不断寻找有理数
为正整数)不断寻找有理数 ,
, ,使得
,使得 ,并且让
,并且让 的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小
的值越来越小,同时利用数轴工具将任务几何化,直观理解通过等分线段的方法不断缩小 对应的点
对应的点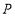 所在线段的长度(二分法)
所在线段的长度(二分法) 思路
在数轴上记
 ,
, 对应的点分别为
对应的点分别为 ,
, 和
和 的平均数
的平均数 对应线段
对应线段 的中点(记为
的中点(记为 ).通过判断
).通过判断 还是
还是 ,得到点
,得到点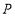 是在二等分后的“左线段
是在二等分后的“左线段 ”上还是“右线段
”上还是“右线段 ”上,重复上述步骤,不断得到
”上,重复上述步骤,不断得到 ,从而得到
,从而得到 更精确的近似值.
更精确的近似值.具体操作步骤及填写“阅读活动任务单”:
(1)当
 时,
时,①寻找左右界值:先寻找两个连续正整数
 ,使得
,使得 .
.因为
 ,所以
,所以 ,那么
,那么 ,
, ,线段
,线段 的中点
的中点 对应的数
对应的数 .
.②二分定位:判断点
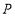 在“左线段
在“左线段 ”上还是在“右线段
”上还是在“右线段 ”上.
”上.比较7与
 的大小,从而确定
的大小,从而确定 与
与 的大小;
的大小;因为
 >
>  (填 “>”或“<”),得到点
(填 “>”或“<”),得到点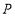 在线段
在线段  上(填“
上(填“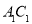 ”或“
”或“ ”).
”).(2)当
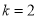 时,在(1)中所得
时,在(1)中所得 的基础上,仿照以上步骤,继续进行下去,得到表中
的基础上,仿照以上步骤,继续进行下去,得到表中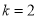 时的相应内容.
时的相应内容.请继续仿照以上步骤操作下去,补全“阅读活动任务单”:



 的值
的值 还是
还是
点
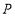 在“左线段
在“左线段 ”上还是“右线段
”上还是“右线段 ”上
”上得出更精确的
 与
与 ,
, ,
, 的大小关系
的大小关系1
2
3
2.5

点
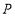 在线段
在线段 上
上
2
2.5
3
2.75

点
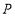 在线段
在线段 上
上
3
2.5
2.75
2.625

4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这
 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.

(1)出发2秒后,求PQ的长;
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点E、F在AC上,且AF=CE,点G、H分别在AB、CD上,且AG=CH,AC与GH相交于点O.
(1)求证:EG//FH;
(2)GH、EF互相平分.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知P为⊙O外一点,PA、PB分别切⊙O于A、B两点,点C为⊙O上一点.
(1)如图1,若AC为直径,求证:OP∥BC;
(2)如图2,若sin∠P=
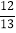 ,求tanC的值.
,求tanC的值.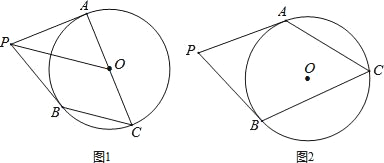
相关试题

