【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系: 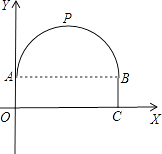
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么?
参考答案:
【答案】
(1)解:由题意可知抛物线的顶点坐标(4,6),
设抛物线的方程为y=a(x﹣4)2+6,
又因为点A(0,2)在抛物线上,
所以有2=a(0﹣4)2+6.
所以a=﹣ ![]() .
.
因此有:y=﹣ ![]() +6
+6
(2)解:令y=4,则有4=﹣ ![]() +6,
+6,
解得x1=4+2 ![]() ,x2=4﹣2
,x2=4﹣2 ![]() ,
,
|x1﹣x2|=4 ![]() >2,
>2,
∴货车可以通过
(3)解:由(2)可知 ![]() |x1﹣x2|=2
|x1﹣x2|=2 ![]() >2,
>2,
∴货车可以通过
【解析】(1)设出抛物线的解析式,根据抛物线顶点坐标,代入解析式;(2)令y=4,解出x与2作比较;(3)隧道内设双行道后,求出横坐标与2作比较.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰三角形△ABC中,AC=BC,D、E分别为AB、BC上一点,∠CDE=∠A.
(1)如图,若BC=BD,求证:CD=DE;
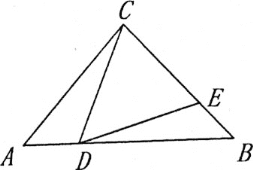
(2)如图,过点C作CH⊥DE,垂足为H,若CD=BD,
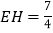 ,直接写出CE-BE的值为________.
,直接写出CE-BE的值为________.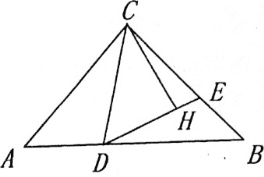
-
科目: 来源: 题型:
查看答案和解析>>【题目】己知:在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.
(1)如图,若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB、AC与PB之间的数量关系,并对你的结论加以证明;

(2)如图,若∠ABC=60°-α,点P在△ABC的内部,且使∠CBP=30°,直接写出∠APC的度数________(用含α的代数式表示).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
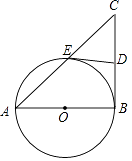
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,点D的坐标是(0,
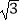 ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
(1)求A,B,C三点的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,∠BAC=90°.
(1)如图,若CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论
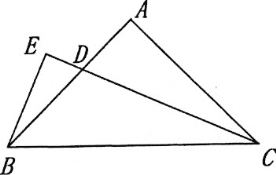
(2)如图,若点D在线段BC延长上,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE和FD的数量关系,并证明你的结论.
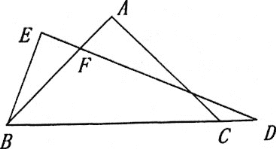
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下面的四个三角形中,不能由如图的三角形经过旋转或平移得到的是( )

A.
B.
C.
D.
相关试题

