【题目】已知△ABC中,AB=AC,∠BAC=90°.
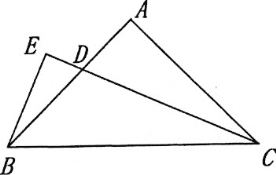
(1)如图,若CD平分∠ACB,BE⊥CD,垂足E在CD的延长线上,试探究线段BE和CD的数量关系,并证明你的结论
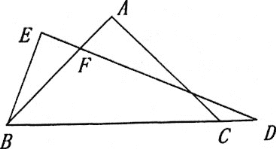
(2)如图,若点D在线段BC延长上,BE⊥DE,垂足为E,DE与AB相交于点F.试探究线段BE和FD的数量关系,并证明你的结论.
参考答案:
【答案】(1)CD=2BE,证明见解析;(2)DF=2BE,证明见解析.
【解析】
(1)如图,证明△ABF≌△ACD,得CD=BF,则2BE=CD;
(2)如图,同(1)作辅助线,证明△BHG≌△DHF得DF=BG=2BE.
(1) 延长BE、CA交于点E
∵CE⊥BF, CD平分∠ACB
∴△BCE为等腰三角形, ∴BF=2BE
易证∠ACD=∠ABF
在△ABF和△ACD中
∴△ABF≌△ACD…………………5分
∴CD=BF=2BE.

(2)过D作DG∥AC交BE的延长线于G,BA的延长线于H
∴∠GDB=∠ACB=∠ABC
BH=DH
同(1)法证在△BHG≌△DHF得DF=BG=2BE.
 .
.
-
科目: 来源: 题型:
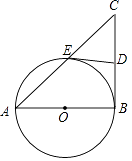
查看答案和解析>>【题目】已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于E点,D为BC的中点.求证:DE与⊙O相切.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一座隧道的截面由抛物线和长方形构成,长方形的长为8m,宽为2m,隧道最高点P位于AB的中央且距地面6m,建立如图所示的坐标系:
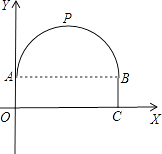
(1)求抛物线的解析式;
(2)一辆货车高4m,宽2m,能否从该隧道内通过,为什么?
(3)如果隧道内设双行道,那么这辆货车是否可以顺利通过,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是菱形,点D的坐标是(0,
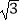 ),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.
),以点C为顶点的抛物线y=ax2+bx+c恰好经过x轴上A,B两点.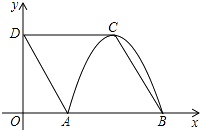
(1)求A,B,C三点的坐标;
(2)求过A,B,C三点的抛物线的解析式;
(3)若将上述抛物线沿其对称轴向上平移后恰好过D点,求平移后抛物线的解析式,并指出平移了多少个单位. -
科目: 来源: 题型:
查看答案和解析>>【题目】在下面的四个三角形中,不能由如图的三角形经过旋转或平移得到的是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,对称轴x=﹣1,下列五个代数式ab、ac、a﹣b+c、b2﹣4ac、2a+b中,值大于0的个数为( )
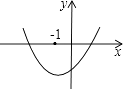
A.5
B.4
C.3
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,直线AB交y轴于A点,交X轴于B点,A(0,6),B(6,0).点D是线段BO上一点,BN⊥AD交AD的延长线于点N.
(1)如图,若OM∥BN交AD于点M.点O作0G⊥BN,交BN的延长线于点G,求证:AM=BG

(2)如图,若∠ADO=67.5°,OM∥BN交AD于点M,交AB于点Q,求
 的值.
的值.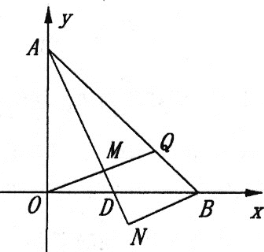
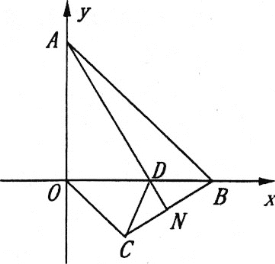
(3)如图,若OC∥AB交BN的延长线于点C.请证明:∠CDN+2∠BDN=180°.
相关试题

