【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴. 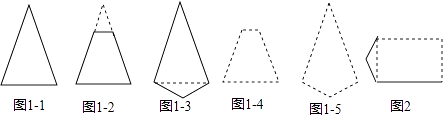
参考答案:
【答案】
(1)1;2;3
(2)解:恰好有1条对称轴的凸五边形如图中所示.
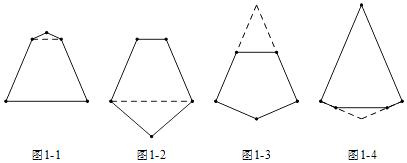
(3)解:恰好有2条对称轴的凸六边形如图所示.
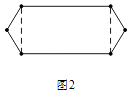
(4)解:恰好有3条对称轴的凸六边形如图所示.
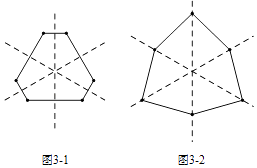
【解析】解:(1)非等边的等腰三角形有1条对称轴,非正方形的长方形有2条对称轴,等边三角形有3条对称轴, 故答案为:1,2,3;
(1)根据等腰三角形的性质、矩形的性质以及等边三角形的性质进行判断即可;(2)中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,在图1﹣4和图1﹣5中,分别仿照类似的修改方式进行画图即可;(3)长方形具有两条对称轴,在长方形的右侧补出与左侧一样的图形,即可构造出一个恰好有2条对称轴的凸六边形;(4)在等边三角形的基础上加以修改,即可得到恰好有3条对称轴的凸六边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC于G (已知)
∴∠ADC=∠EGC=90°
∴AD∥EG .
∴∠1=∠2 .
=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3 .
∴AD平分∠BAC .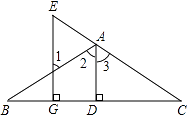
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
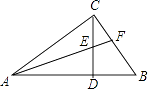
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知M=
 是m+3的算术平方根,N=
是m+3的算术平方根,N=  是n﹣2的立方根,试求M﹣N的值.
是n﹣2的立方根,试求M﹣N的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,
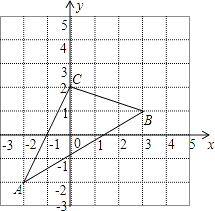
(1)请写出△ABC各点的坐标.
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出 A′、B′、C′的坐标,并在图中画出平移后图形.
(3)求出三角形ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x2﹣2x+k=0有实数根,则k的取值范围是( )
A. k<1B. k<4C. k≤1D. k≤4
相关试题

