【题目】如图,已知:AD⊥BC于D,EG⊥BC于G,∠E=∠1.求证:AD平分∠BAC.
下面是部分推理过程,请你将其补充完整:
∵AD⊥BC于D,EG⊥BC于G (已知)
∴∠ADC=∠EGC=90°
∴AD∥EG .
∴∠1=∠2 .
=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3 .
∴AD平分∠BAC . 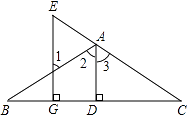
参考答案:
【答案】同位角相等,两直线平行;两直线平行,内错角相等;∠E;等量代换;角平分线的定义
【解析】解:∵AD⊥BC于D,EG⊥BC于G (已知)
∴∠ADC=∠EGC=90°
∴AD∥EG,(同位角相等,两直线平行).
∴∠1=∠2,(两直线平行,内错角相等).
∠E=∠3(两直线平行,同位角相等)
又∵∠E=∠1(已知)
∴∠2=∠3,(等量代换).
∴AD平分∠BAC.(角平分线的定义)
所以答案是:同位角相等,两直线平行;两直线平行,内错角相等;∠E;等量代换;角平分线的定义.
【考点精析】掌握垂线的性质和平行线的判定与性质是解答本题的根本,需要知道垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2019年广东省政府工作报告中指出:我省大力实施乡村振兴战略,加快解决农业农村突出问题,“三农”工作取得新成效,省财政自2018年起三年投入75亿元支持粤东粤西粤北省级现代农业产业园建设.用科学记数法表示75亿为( )
A. 7.5×108B. 0.75×1010C. 75×108D. 7.5×109
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程2x2﹣4x+(m﹣1)=0有两个不相等的实数根,则m的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,CE平分∠BCF,∠DAC=116°,∠ACF=25°,求∠FEC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ACB中,∠ACB=90゜,CD⊥AB于D.
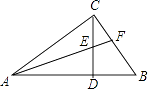
(1)求证:∠ACD=∠B;
(2)若AF平分∠CAB分别交CD、BC于E、F,求证:∠CEF=∠CFE. -
科目: 来源: 题型:
查看答案和解析>>【题目】在我们认识的多边形中,有很多轴对称图形.有些多边形,边数不同对称轴的条数也不同;有些多边形,边数相同但却有不同数目的对称轴.回答下列问题:
(1)非等边的等腰三角形有条对称轴,非正方形的长方形有条对称轴,等边三角形有条对称轴;
(2)观察下列一组凸多边形(实线画出),它们的共同点是只有1条对称轴,其中图1﹣2和图1﹣3都可以看作由图1﹣1修改得到的,仿照类似的修改方式,请你在图1﹣4和图1﹣5中,分别修改图1﹣2和图1﹣3,得到一个只有1条对称轴的凸五边形,并用实线画出所得的凸五边形;
(3)小明希望构造出一个恰好有2条对称轴的凸六边形,于是他选择修改长方形,图2中是他没有完成的图形,请用实线帮他补完整个图形;
(4)请你画一个恰好有3条对称轴的凸六边形,并用虚线标出对称轴.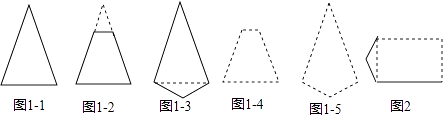
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M=
 是m+3的算术平方根,N=
是m+3的算术平方根,N=  是n﹣2的立方根,试求M﹣N的值.
是n﹣2的立方根,试求M﹣N的值.
相关试题

