【题目】我们规定:若关于x的方程ax=b的解为x=b-a,则称该方程为“差解方程”.例如:2x=4的解为x=2,且2=4-2,则2x=4是“差解方程”.
(1)判断3x=4.5是不是“差解方程”;
(2)若关于x的方程2x=4m+6是“差解方程”,求m的值.
参考答案:
【答案】(1)3x=4.5是“差解方程”;(2)![]() .
.
【解析】
(1)根据“差解方程”的定义判断即可;
(2)根据“差解方程”的定义列出关于m的方程求解即可.
解:(1)因为3x=4.5,
所以x=1.5.
又因为4.5-3=1.5,
所以3x=4.5是“差解方程”.
(2)因为2x=4m+6,所以x=2m+3.
又因为关于x的方程2x=4m+6是“差解方程”,
所以2m+3=4m+6-2,
解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】当ab>0时,y=ax2与y=ax+b的图象大致是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=ax+b与二次函数y=bx2+a的图象可能是( )
A.
B.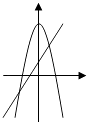
C.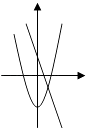
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数中,当x>0时,y的值随x的值增大而增大的是( )
A.y=﹣x2
B.y=x﹣1
C.y=﹣x+1
D.y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB过x轴上一点A(2,0),且与抛物线y=ax2相交于B、C两点,B点坐标为(1,1).

(1)求直线AB的解析式及抛物线y=ax2的解析式;
(2)求点C的坐标;
(3)求S△COB . -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c (a、b、c为常数且a≠0)中的x与y的部分对应值如下表,
x
…
-3
-2
-1
0
1
2
3
4
5
…
y
…
12
5
0
-3
-4
-3
0
5
12
…
下列四个结论:
①二次函数y=ax2+bx+c 有最小值,最小值为-3;
②抛物线与y轴交点为(0,-3);
③二次函数y=ax2+bx+c 的图像对称轴是x=1;
④本题条件下,一元二次方程ax2+bx+c的解是x1=-1,x2=3.
其中正确结论的个数是( )
A.4
B.3
C.2
D.1 -
科目: 来源: 题型:
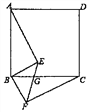
查看答案和解析>>【题目】如图,四边形ABCD是正方形,BE⊥BF,BE=BF,EF与BC交于点G.
(1)求证:AE=CF;
(2)若∠ABE=55°,求∠EGC的大小.
相关试题

