【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα= ![]() ,则线段CE的最大值为 .
,则线段CE的最大值为 . 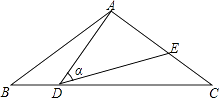
参考答案:
【答案】6.4
【解析】解:作AG⊥BC于G,如图,
∵AB=AC,
∴BG=CG,
∵∠ADE=∠B=α,
∴cosB=cosα= ![]() =
= ![]() ,
,
∴BG= ![]() ×10=8,
×10=8,
∴BC=2BG=16,
设BD=x,则CD=16﹣x,
∵∠ADC=∠B+∠BAD,即α+∠CDE=∠B+∠BAD,
∴∠CDE=∠BAD,
而∠B=∠C,
∴△ABD∽△DCE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴CE=﹣ ![]() x2+
x2+ ![]() x
x
=﹣ ![]() (x﹣8)2+6.4,
(x﹣8)2+6.4,
当x=8时,CE最大,最大值为6.4.
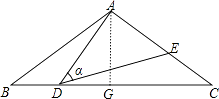
作AG⊥BC于G,如图,根据等腰三角形的性质得BG=CG,再利用余弦的定义计算出BG=8,则BC=2BG=16,设BD=x,则CD=16﹣x,证明△ABD∽△DCE,利用相似比可表示出CE=﹣ ![]() x2+
x2+ ![]() x,然后利用二次函数的性质求CE的最大值.
x,然后利用二次函数的性质求CE的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空;
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
3
1
1
2
3
…
②描点;
③连线.
(2)观察图象,当x 时,y随x的增大而增大;
(3)根据图象,不等式|x|<
 x+
x+ 的解集为 .
的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形
 中,已知
中,已知 ,
, ,且
,且 .
.
(1)填空:
 _____,
_____, ______,
______, _______;
_______;(2)点
 为射线
为射线 上一任意一点,连接
上一任意一点,连接 ,作
,作 的平分线
的平分线 ,交射线
,交射线 于点
于点 ,作
,作 的平分线
的平分线 ,交直线
,交直线 于点
于点 ,请探究射线
,请探究射线 与
与 之间的位置关系,并加以证明;
之间的位置关系,并加以证明;(3)连接
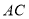 ,若
,若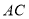 恰好平分
恰好平分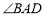 ,则在(2)问的条件下,是否存在角度
,则在(2)问的条件下,是否存在角度 ,使得当
,使得当 时,有
时,有 (其中
(其中 为不超过10的正整数)?若存在,求出
为不超过10的正整数)?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 的坐标为
的坐标为 ,以 A 为顶点的
,以 A 为顶点的 的两边始终与
的两边始终与  轴交于
轴交于  、
、 两点(
两点( 在
在  左面),且
左面),且 .
.(1)如图,连接
 ,当
,当  时,试说明:
时,试说明: .
.
(2)过点
 作
作 轴,垂足为
轴,垂足为 ,当
,当 时,将
时,将 沿
沿 所在直线翻折,翻折后边
所在直线翻折,翻折后边 交
交  轴于点
轴于点  ,求点
,求点  的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】百年大计,教育为本.为了让贫困地区的孩子也能接受公平、有质量的教育,某中学学生积极响应号召,计划向某山区贫困中小学生进行捐助,捐助总人数为23名.资助一名中学生的学习费用需
 元,一名小学生的学习费用需
元,一名小学生的学习费用需 元,初中各年级学生捐款数额与其恰好捐助贫困中学生和小学生人数的部分情况如下表:
元,初中各年级学生捐款数额与其恰好捐助贫困中学生和小学生人数的部分情况如下表:年级
捐款数额(元)
捐助贫困中学生人数(名)
捐助贫困小学生人数(名)
初一年级
4000
2
4
初二年级
4200
3
3
初三年级
7400
(1)求
 的值;
的值;(2)初三学生的全部捐款用于解决余下(部分或全部)的贫困中小学生的学习费用,求初三年级学生可捐助的贫困中、小学生人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】高空抛物极其危险,是我们必须杜绝的行为.据研究,高空抛物下落的时间t(单位:s)和高度 h(单位:m)近似满足公式 t=
 (不考虑风速的影响)
(不考虑风速的影响)(1)从 50m 高空抛物到落地所需时间 t1 是多少 s,从 100m 高空抛物到落地所 需时间 t2 是多少 s;
(2)t2 是 t1 的多少倍?
(3)经过 1.5s,高空抛物下落的高度是多少?

相关试题

