【题目】如图,在四边形![]() 中,已知
中,已知![]() ,
,![]() ,且
,且![]() .
.

(1)填空:![]() _____,
_____,![]() ______,
______,![]() _______;
_______;
(2)点![]() 为射线
为射线![]() 上一任意一点,连接
上一任意一点,连接![]() ,作
,作![]() 的平分线
的平分线![]() ,交射线
,交射线![]() 于点
于点![]() ,作
,作![]() 的平分线
的平分线![]() ,交直线
,交直线![]() 于点
于点![]() ,请探究射线
,请探究射线![]() 与
与![]() 之间的位置关系,并加以证明;
之间的位置关系,并加以证明;
(3)连接![]() ,若
,若![]() 恰好平分
恰好平分![]() ,则在(2)问的条件下,是否存在角度
,则在(2)问的条件下,是否存在角度![]() ,使得当
,使得当![]() 时,有
时,有![]() (其中
(其中![]() 为不超过10的正整数)?若存在,求出
为不超过10的正整数)?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
参考答案:
【答案】(1)![]() ;
;![]() ;
;![]() (2)
(2)![]() ;证明见详解(3)存在;
;证明见详解(3)存在;![]() 、
、![]() 或
或![]()
【解析】
(1)根据垂直的定义、平行线的性质、四边形的内角和即可得解;
(2)按照题目要求画出图形后,根据已知条件、角平分线的性质、平行线的性质和判定即可得到结论并证明;
(3)结合图形根据平行线的性质、角平分线的性质、角的和差可列出![]() ,再由
,再由![]() 、
、![]() 的取值范围即可求得结论.
的取值范围即可求得结论.
解:(1)∵![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]() ;
;
(2)按照题目要求作图:
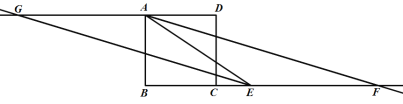
猜想:射线![]() 与
与![]() 的位置关系是:
的位置关系是:![]()
证明: ∵![]() 平分
平分![]() ,
,![]() 平分
平分![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴![]()
∴![]() ;
;
(3)在(2)问的条件下,连接![]() ,如图:
,如图:
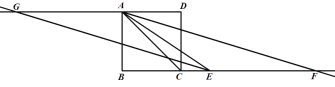
∵![]() ,
,![]()
∴![]() ,
,![]()
∴![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]() 恰好平分
恰好平分![]() ,由(1)可知
,由(1)可知![]()
∴![]()
∵![]() 为射线
为射线![]() 上一任意一点
上一任意一点
∴![]()
∵![]() 为不超过10的正整数
为不超过10的正整数
∴当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
∴存在角度![]() ,使得当
,使得当![]() 时,有
时,有![]() (其中
(其中![]() 为不超过10的正整数);
为不超过10的正整数);![]() 、
、![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪和小明沿同一条笔直的马路同时从学校出发到某图书馆查阅资料,学校与 图书馆的路程是
 千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线
千米,小聪骑自行车,小明步行,当小聪从原路回到学校时,小明刚好到 达图书馆,图中折线  和线段
和线段  分别表示两人离学校的路程
分别表示两人离学校的路程  (千米)与所经过的 时间
(千米)与所经过的 时间  (分钟)之间的函数关系,请根据图像回答下列问题:
(分钟)之间的函数关系,请根据图像回答下列问题:(1)小聪在图书馆查阅资料的时间为 分钟;小聪返回学校的速度为 千米/分钟.
(2)请你求出小明离开学校的路程
 (千米)与所经过的时间
(千米)与所经过的时间  (分钟)之间的函数表达式;
(分钟)之间的函数表达式;(3)若设两人在路上相距不超过
 千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
千米时称为可以“互相望见”,则小聪和小明可以“互相 望见”的时间共有多少分钟?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价
成本价
销售价(元/箱)
甲
24
36
乙
33
48
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请你用学习“一次函数”时积累的经验和方法研究函数y=|x|的图象和性质,并解决问题.
(1)完成下列步骤,画出函数y=|x|的图象;
①列表、填空;
x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
3
1
1
2
3
…
②描点;
③连线.
(2)观察图象,当x 时,y随x的增大而增大;
(3)根据图象,不等式|x|<
 x+
x+ 的解集为 .
的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点
 的坐标为
的坐标为 ,以 A 为顶点的
,以 A 为顶点的 的两边始终与
的两边始终与  轴交于
轴交于  、
、 两点(
两点( 在
在  左面),且
左面),且 .
.(1)如图,连接
 ,当
,当  时,试说明:
时,试说明: .
.
(2)过点
 作
作 轴,垂足为
轴,垂足为 ,当
,当 时,将
时,将 沿
沿 所在直线翻折,翻折后边
所在直线翻折,翻折后边 交
交  轴于点
轴于点  ,求点
,求点  的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=
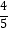 ,则线段CE的最大值为 .
,则线段CE的最大值为 . 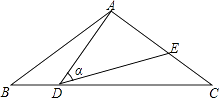
-
科目: 来源: 题型:
查看答案和解析>>【题目】百年大计,教育为本.为了让贫困地区的孩子也能接受公平、有质量的教育,某中学学生积极响应号召,计划向某山区贫困中小学生进行捐助,捐助总人数为23名.资助一名中学生的学习费用需
 元,一名小学生的学习费用需
元,一名小学生的学习费用需 元,初中各年级学生捐款数额与其恰好捐助贫困中学生和小学生人数的部分情况如下表:
元,初中各年级学生捐款数额与其恰好捐助贫困中学生和小学生人数的部分情况如下表:年级
捐款数额(元)
捐助贫困中学生人数(名)
捐助贫困小学生人数(名)
初一年级
4000
2
4
初二年级
4200
3
3
初三年级
7400
(1)求
 的值;
的值;(2)初三学生的全部捐款用于解决余下(部分或全部)的贫困中小学生的学习费用,求初三年级学生可捐助的贫困中、小学生人数.
相关试题

