【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2![]() cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.

参考答案:
【答案】(1) 若0<t≤5,则AP=4t,AQ=2t. 则 ==,
又 ∵ AO=10,AB=20,∴ ==.∴ =,
又 ∠CAB=30°,∴ △APQ∽△ABO,∴ ∠AQP=90°,即PQ⊥AC. ………………4分
当5﹤t≤10时,同理可由△PCQ∽△BCO 可得∠PQC=90°,即PQ⊥AC(考虑一种情况即可)
∴ 在点P、Q运动过程中,始终有PQ⊥AC.
(2)① 如图,在RtAPM中,易知AM=,又AQ=2t,
QM=20-4t.
由AQ+QM=AM 得2t+20-4t=
解得t=,∴ 当t=时,点P、M、N在一直线上. …………………………8分
② 存在这样的t,使△PMN是以PN为一直角边的直角三角形.
设l交AC于H.
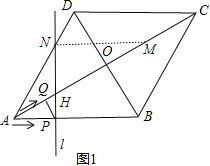
如图1,当点N在AD上时,若PN⊥MN,则∠NMH=30°.
∴ MH=2NH,得 20-4t-=2× 解得t=2, …………………10分
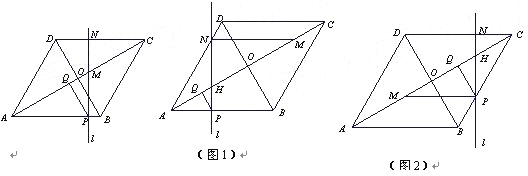
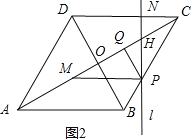
如图2,当点N在CD上时,若PM⊥MN,则∠HMP=30°.∴ MH=2PH,同理可得t= .
故 当t=2或 时,存在以PN为一直角边的直角三角形. …………………12分
【解析】
(1)此问需分两种情况,当0<t≤5及5<t≤10两部分分别讨论得PQ⊥AC.
(2)①由于点P、M、N在一直线上,则AQ+QM=AM,代入求得t的值.
②假设存在这样的t,使得△PMN是以PN为一直角边的直角三角形,但是需分点N在AD上时和点N在CD上时两种情况分别讨论.
解答:解:(1)若0<t≤5,则AP=4t,AQ=2![]() t.
t.
则![]() =
=![]() =
=![]() ,
,
又∵AO=10![]() ,AB=20,∴
,AB=20,∴![]() =
=![]() =
=![]() .
.
∴![]() =
=![]() .又∠CAB=30°,∴△APQ∽△ABO.
.又∠CAB=30°,∴△APQ∽△ABO.
∴∠AQP=90°,即PQ⊥AC.
当5<t≤10时,同理,可由△PCQ∽△BCO得∠PQC=90°,即PQ⊥AC.
∴在点P、Q运动过程中,始终有PQ⊥AC.
(2)①如图,在Rt△APM中,∵∠PAM=30°,AP=4t,
∴AM=![]() .
.
在△APQ中,∠AQP=90°,
∴AQ=AP?cos30°=2![]() t,
t,
∴QM=AC-2AQ=20![]() -4
-4![]() t.
t.
由AQ+QM=AM得:2![]() t+20
t+20![]() -4
-4![]()
t=![]() ,
,
解得t=![]() .
.
∴当t=![]() 时,点P、M、N在一直线上.
时,点P、M、N在一直线上.

②存在这样的t,使△PMN是以PN为一直角边的直角三角形.
设l交AC于H.
如图1,当点N在AD上时,若PN⊥MN,则∠NMH=30°.
∴MH=2NH.得20![]() -4
-4![]() t-
t-![]() t=2×
t=2×![]() ,解得t=2.
,解得t=2.
如图2,当点N在CD上时,若PM⊥PN,则∠HMP=30°.
∴MH=2PH,同理可得t=![]() .
.
故当t=2或![]() 时,存在以PN为一直角边的直角三角形.
时,存在以PN为一直角边的直角三角形.
-
科目: 来源: 题型:
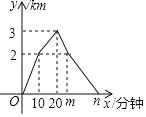
查看答案和解析>>【题目】小明和爸爸周末到湿地公园进行锻炼,两人同时从家出发,匀速骑共享单车到达公园入口,然后一同匀速步行到达驿站,到达驿站后小明的爸爸立即又骑共享单车按照来时骑行速度原路返回,在公园入口处改为步行,并按来时步行速度原路回家,小明到达驿站后逗留了10分钟之后骑车回家,爸爸在锻炼过程中离出发地的路程与出发的时间的函数关系如图.
(1)图中m=_____,n=_____;(直接写出结果)
(2)小明若要在爸爸到家之前赶上,问小明回家骑行速度至少是多少?
-
科目: 来源: 题型:
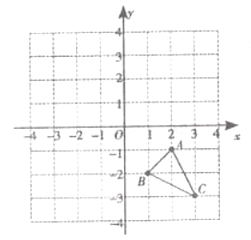
查看答案和解析>>【题目】如图:在平面直角坐标系中,已知
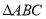 的三个顶点的坐标分别为
的三个顶点的坐标分别为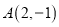 ,
,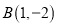 ,
,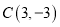 .
.
(1)将
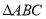 向上平移
向上平移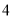 个单位长度,再向左平移
个单位长度,再向左平移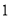 个单位长度,得到
个单位长度,得到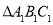 ,请画出
,请画出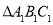 (点
(点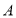 ,
,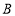 ,
,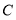 的对应点分别为
的对应点分别为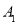 ,
,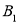 ,
,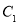 )
)(2)请画出与
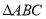 关于
关于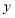 轴对称的
轴对称的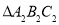 (点
(点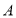 ,
,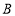 ,
,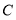 的对应点分别为
的对应点分别为 ,
,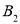 ,
,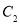 )
)(3)请写出
 ,
, 的坐标
的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=mx+3的图象经过点A(2,6),B(n,-3).求:
(1)m,n的值;
(2)△OAB的面积.

-
科目: 来源: 题型:
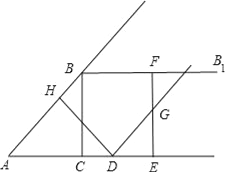
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=
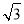 AE;
AE;(2)当α=90°时(如图2),求
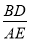 的值.
的值.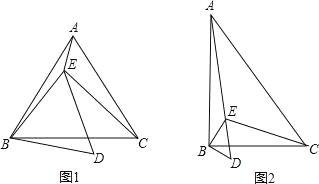
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
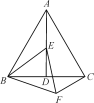
(1)求证:AE=CF;
(2)求∠ACF的度数.
相关试题

