【题目】如图,在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积. 某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路,完成解答过程.
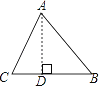
(1)作AD⊥BC于D,设BD=x,用含x的代数式表示CD,则CD=________;
(2)请根据勾股定理,利用AD作为“桥梁”建立方程,并求出x的值;
(3)利用勾股定理求出AD的长,再计算三角形的面积.
参考答案:
【答案】(1)14﹣x;(2)9;(3)84
【解析】试题分析:(1)已知BC=14,设BD=x,则CD=BC-BD=14-x;(2)在 Rt△ABD 中,根据勾股定理求得AD,在 Rt△ACD 中,根据勾股定理求得AD,代入数据列出方程,解方程即可;(3)在(2)的基础上求得AD的长,再利用三角形的面积公式求解即可.
试题解析:
(1)CD=(14-x)
(2)∵ AD 是 BC 边上的高,
∴△ABD 和△ACD 都是直角三角形.
在 Rt△ABD 中,根据勾股定理,AD=AB-BD=15-x
在 Rt△ACD 中,根据勾股定理,得AD=AC-CD=13-(14-x)
∴15-x=13-(14-x)
解得:x=9,即BD=9.
(3)AD=15-9=225-81=144,∴AD=12
所以![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图所示,AB//CD,点E在AD的延长线上,∠EDC与∠B互为补角.
(1)问AD,BC是否平行?请说明理由;
(2)如果∠EDC=72°,∠1=∠2=2∠CAB,求∠CAF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两艘轮船同时从港口O出发,甲轮船以20海里/时的速度向南偏东45°方向航行,乙轮船向南偏西45°方向航行.已知它们离开港口O两小时后,两艘轮船相距50海里,求乙轮船平均每小时航行多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在双曲线y=
 上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC﹣AC=2,则k的值为( )
上,且OA=4,过点A作AC⊥x轴,垂足为C,OA的垂直平分线交OC于点B,如果AB+BC﹣AC=2,则k的值为( ) 
A.8﹣2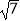
B.8+2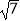
C.3
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,若点P(4,0)在该抛物线上,则一元二次方程ax2+bx+c=0的两根为 .
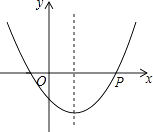
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

-
科目: 来源: 题型:
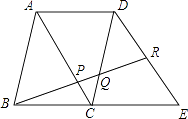
查看答案和解析>>【题目】如图,四边形ABCD和四边形ACED都是平行四边形,点R在DE上,且DR:RE=5:4,BR分别与AC,CD相交于点P,Q,则BP:PQ:QR= .
相关试题

