【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图像如图所示,根据图像所提供的信息解答下列问题: 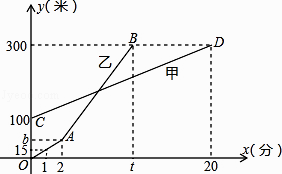
(1)甲登山上升的速度是每分钟米,乙在A地时距地面的高度b为米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式.
(3)登山多长时间时,甲、乙两人距地面的高度差为50米?
参考答案:
【答案】
(1)10;30
(2)解:当0≤x≤2时,y=15x;
当x≥2时,y=30+10×3(x﹣2)=30x﹣30.
当y=30x﹣30=300时,x=11.
∴乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y= ![]()
(3)解:甲登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式为y=10x+100(0≤x≤20).
当10x+100﹣(30x﹣30)=50时,解得:x=4;
当30x﹣30﹣(10x+100)=50时,解得:x=9;
当300﹣(10x+100)=50时,解得:x=15.
答:登山4分钟、9分钟或15分钟时,甲、乙两人距地面的高度差为50米
【解析】解:(1)(300﹣100)÷20=10(米/分钟),b=15÷1×2=30.故答案为:10;30.(1)根据速度=高度÷时间即可算出甲登山上升的速度;根据高度=速度×时间即可算出乙在A地时距地面的高度b的值;(2)分0≤x≤2和x≥2两种情况,根据高度=初始高度+速度×时间即可得出y关于x的函数关系;(3)找出甲登山全程中y关于x的函数关系式,令二者做差等于50即可得出关于x的一元一次方程,解之即可得出结论.
-
科目: 来源: 题型:
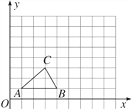
查看答案和解析>>【题目】如图,在9×9网格中,每个小方格的边长看作单位1,每个小方格的顶点叫作格点,△ABC的顶点都在格点上.
(1)请在网格中画出△ABC的一个位似图形△A1B1C,使两个图形以点C为位似中心,且所画图形与△ABC的相似比为2∶1;
(2)将△A1B1C绕着点C顺时针旋转90°得△A2B2C,画出图形,并在如图所示的坐标系中分别写出△A2B2C三个顶点的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司派出甲车前往某地完成任务,此时,有一辆流动加油车与他同时出发,且在同一条公路上匀速行驶(速度保持不变).为了确定汽车的位置,我们用OX表示这条公路,原点O为零千米路标,并作如下约定:速度为正,表示汽车向数轴的正方向行驶;速度为负,表示汽车向数轴的负方向行驶;速度为零,表示汽车静止.行程为正,表示汽车位于零千米的右侧;行程为负,表示汽车位于零千米的左侧;行程为零,表示汽车位于零千米处.两车行程记录如表:

由上面表格中的数据,解决下列问题:
(1)甲车开出7小时时的位置为 km,流动加油车出发位置为 km;
(2)当两车同时开出x小时时,甲车位置为 km,流动加油车位置为 km (用x的代数式表示);
(3)甲车出发前由于未加油,汽车启动后司机才发现油箱内汽油仅够行驶3小时,问:甲车连续行驶3小时后,能否立刻获得流动加油车的帮助?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡行走20m,到达坡顶D处,已知斜坡的坡角为15°.(sin15°=0.259,cos15°=0.966,tan15°=0.268,以下计算结果精确到0.1m)
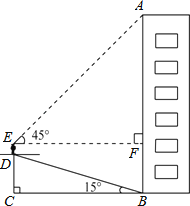
(1)求小华此时与地面的垂直距离CD的值;
(2)小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.
-
科目: 来源: 题型:
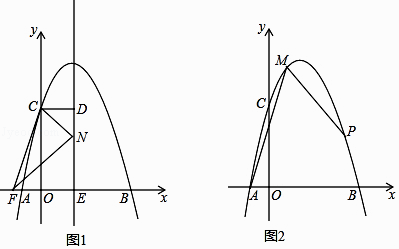
查看答案和解析>>【题目】二次函数y=ax2+bx+4的图像与x轴交于两点A、B,与y轴交于点C,且A(﹣1,0)、B(4,0)
(1)求此二次函数的表达式
(2)如图1,抛物线的对称轴m与x轴交于点E,CD⊥m,垂足为D,点F(﹣ ,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标
,0),动点N在线段DE上运动,连接CF、CN、FN,若以点C、D、N为顶点的三角形与△FEN相似,求点N的坐标
(3)如图2,点M在抛物线上,且点M的横坐标是1,点P为抛物线上一动点,若∠PMA=45°,求点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)x2y﹣3xy2+2x2y﹣y2x ;(2)2(2a2﹣9b)﹣3(3a2﹣7b);
(3)2a2﹣[
 (ab﹣4a2)+8ab]﹣
(ab﹣4a2)+8ab]﹣ ab.
ab. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=4,tan∠ACB=
 ,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为______.
,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于点F,则四边形AFBD的面积为______.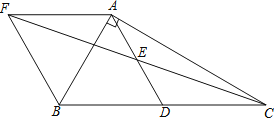
相关试题

