【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想; 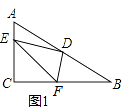
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明) 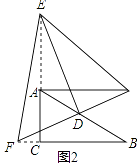
参考答案:
【答案】
(1)结论:AE2+BF2=EF2.
理由:如图1中,延长FD到M,使得DM=DF,连接AM,EM.
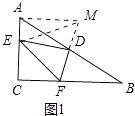
在△ADM和△BDF中,
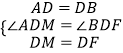 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2,
∴AE2+BF2=EF2.
(2)如图2中,结论不变.AE2+BF2=EF2
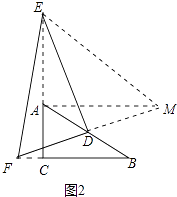
理由:延长FD到M,使得DM=DF,连接AM,EM.
在△ADM和△BDF中,
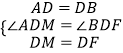 ,
,
∴△ADM≌△BDF,
∴AM=BF,∠B=∠MAD,
∵∠C=90°,
∴∠B+∠CAB=90°,
∴∠CAB+∠MAD=90°,即∠EAM=∠CAM=90°,
∵∠EDF=90°,
∴ED⊥FM,∵DM=DF,
∴EM=EF,
在Rt△AEM中,∵AE2+AM2=EM2,
∴AE2+BF2=EF2.
【解析】(1)结论:AE2+BF2=EF2 . 如图1中,延长FD到M,使得DM=DF,连接AM,EM.首先证明△ADM≌△BDF,得到AM=FB,再证明△AEM是直角三角形,理由勾股定理即可解决问题.(2)结论不变,证明方法类似.
【考点精析】关于本题考查的直角三角形斜边上的中线,需要了解直角三角形斜边上的中线等于斜边的一半才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算或化简
(1)﹣22+(﹣ )﹣2﹣(π﹣5)0﹣|﹣3|
)﹣2﹣(π﹣5)0﹣|﹣3|
(2)(﹣3a)3+(﹣2a4)2÷(﹣a)5
(3)(a+3b﹣2c)(a﹣3b﹣2c)
(4)y(x+y)+(x﹣y)2﹣(x+y)(﹣y+x),其中x=﹣ 、y=3.
、y=3. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+mx+9是完全平方式,则常数m等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。

(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使
 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:

(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用一条长为40cm的绳子围成一个面积为acm2的长方形,a的值不可能为( )
A. 20B. 40C. 100D. 120
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成以下任务,适合用抽样调查的是( )
A. 调查你班同学的年龄情况 B. 考察一批炮弹的杀伤半径
C. 为订购校服,了解学生衣服的尺寸 D. 对航天飞机上的零部件进行检查
相关试题

