【题目】计算或化简
(1)﹣22+(﹣ ![]() )﹣2﹣(π﹣5)0﹣|﹣3|
)﹣2﹣(π﹣5)0﹣|﹣3|
(2)(﹣3a)3+(﹣2a4)2÷(﹣a)5
(3)(a+3b﹣2c)(a﹣3b﹣2c)
(4)y(x+y)+(x﹣y)2﹣(x+y)(﹣y+x),其中x=﹣ ![]() 、y=3.
、y=3.
参考答案:
【答案】
(1)解:﹣22+(﹣ ![]() )﹣2﹣(π﹣5)0﹣|﹣3|
)﹣2﹣(π﹣5)0﹣|﹣3|
=﹣4+4﹣1﹣3
=﹣4;
(2)解:(﹣3a)3+(﹣2a4)2÷(﹣a)5
=(﹣27a3)+4a8÷(﹣a5)
=(﹣27a3)﹣4a3
=﹣31a3;
(3)解:(a+3b﹣2c)(a﹣3b﹣2c)
=[(a﹣2c)+3b][(a﹣2c)﹣3b]
=(a﹣2c)2﹣9b2
=a2﹣4ac+4c2﹣9b2;
(4)解:y(x+y)+(x﹣y)2﹣(x+y)(﹣y+x)
=xy+y2+x2﹣2xy+y2﹣x2+y2
=﹣xy+3y2,
当x=﹣ ![]() 、y=3时,原式=
、y=3时,原式= ![]() =28.
=28.
【解析】(1)根据负整数指数幂、零指数幂、绝对值可以解答本题;(2)根据同底数幂的除法和积的乘方可以解答本题;(3)根据平方差公式和完全平方公式可以解答本题;(4)先化简题目中的式子,再将x、y的值代入即可解答本题.
【考点精析】关于本题考查的零指数幂法则和整数指数幂的运算性质,需要了解零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果店卖出的香蕉数量(千克)与售价(元)之间的关系如表:
数量(千克)
0.5
1
1.5
2
2.5
3
3.5
…
售价(元)
1.5
3
4.5
6
7.5
9
10.5
…
上表反映了个变量之间的关系,其中,自变量是;因变量是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x袖于点M , 交y轴于点N , 再分别以点M、N为圆心,大于MN的长为半径画弧,两弧在第二象限交于点P . 若点P的坐标为(2a , b+1),则a与b的数量关系为( )
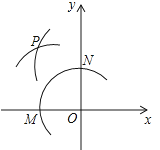
A.a-b
B.2a+b=-1
C.2a-b=l
D.2a+b=l -
科目: 来源: 题型:
查看答案和解析>>【题目】利用计算器求值(精确到0.0001):tan27°15′+cos63°42′=
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x2+mx+9是完全平方式,则常数m等于 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角体系中,直线AB交x轴于点A(5,0),交y轴于点B,AO是⊙M的直径,其半圆交AB于点C,且AC=3。取BO的中点D,连接CD、MD和OC。

(1)求证:CD是⊙M的切线;
(2)二次函数的图象经过点D、M、A,其对称轴上有一动点P,连接PD、PM,求△PDM的周长最小时点P的坐标;
(3)在(2)的条件下,当△PDM的周长最小时,抛物线上是否存在点Q,使
 ?若存在,求出点Q的坐标;若不存在,请说明理由。
?若存在,求出点Q的坐标;若不存在,请说明理由。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,∠ACB=90°,D是AB的中点,∠EDF=90°
(1)如图1,若E、F分别在AC、BC边上,猜想AE2、BF2和EF2之间有何等量关系,并证明你的猜想;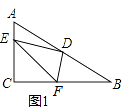
(2)若E、F分别在CA、BC的延长线上,请在图2中画出相应的图形,并判断(1)中的结论是否仍然成立(不作证明)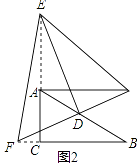
相关试题

