【题目】问题发现:如图1,在△ABC中,∠C=90°,分别以AC,BC为边向外侧作正方形ACDE和正方形BCFG.
(1)△ABC和△DCF面积的关系是______________;(请在横线上填写“相等”或“不等”)
(2)拓展探究:若∠C≠90°,(1)中的结论还成立吗?若成立,请结合图2给出证明;若不成立,请说明理由;
(3)解决问题:如图3,在四边形ABCD中,AC⊥BD,且AC与BD的和为10,分别以四边形ABCD的四条边为边向外侧作正方形ABFE、正方形BCHG、正方形CDJI,正方形DALK,运用(2)的结论,图中阴影部分的面积和是否有最大值?如果有,请求出最大值,如果没有,请说明理由.
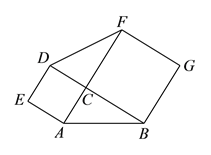
图1
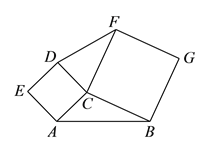
图2
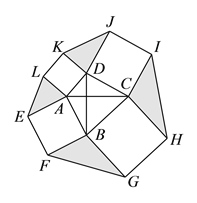
图3
参考答案:
【答案】(1)相等;(2)成立,理由见解析;(3)阴影部分的面积和有最大值,最大值为25
【解析】解:(1)相等;
(2)成立;理由如下:
如图,延长BC到点P,过点A作AP⊥BP于点P;过点D作DQ⊥FC于点Q.
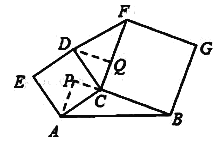
∴∠APC=∠DQC=90°.
∵四边形ACDE、四边形BCFG均为正方形,
∴AC=CD,BC=CF,∠ACP+∠PCD=90°,∠DCQ+∠PCD=90°,
∴∠ACP=∠DCQ.
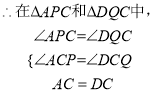
∴△APC≌△DQC(AAS),
∴AP=DQ.
又∵S△ABC=![]() BCAP,S△DFC =
BCAP,S△DFC =![]() FCDQ,
FCDQ,
∴S△ABC=S△DFC.
(3)图中阴影部分的面积和有最大值
理由:由(2)的结论可知:
![]()
![]()
设AC=m,则BD=10-m, ∵AC⊥BD.
∴![]() .
.
∴![]()
∴阴影部分的面积和有最大值,最大值为25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α的余角是32°,∠β的补角是105°,那么2α﹣β=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+3)2+|y﹣2|=0,则(x+y)2017= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:﹣23﹣3×|﹣2|﹣(﹣7+5)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC=90°,∠EBE′=90°,AB=BC,BE=BE′,若AE=1,BE=2,∠BE′C=135°,求EC的长.

-
科目: 来源: 题型:
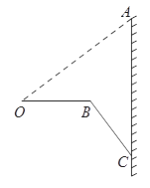
查看答案和解析>>【题目】如图,高铁列车座位后面的小桌板收起时可以近似地看作与地面垂直,展开小桌板后,桌面会保持水平.如图的实线是小桌板展开后的示意图,其中OB表示小桌面的宽度,BC表示小桌板的支架.连接OA,此时OA=75厘米,∠AOB=∠ACB=37°,且支架长BC与桌面宽OB的长度之和等于OA的长度,求点B到AC的距离.(参考数据:
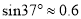 ,
, 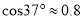 ,
, 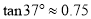 )
)
相关试题

