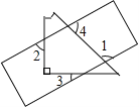
【题目】一直尺与一缺了一角的等腰直角三角板如图摆放,若∠1=115°,则∠2的度数为( )
A.65°B.70°C.75°D.80°
参考答案:
【答案】B
【解析】
先将一缺了一角的等腰直角三角板补全,再由直尺为矩形,则两组对边分别平行,即可根据∠1求∠4的度数,即可求出∠4的对顶角的度数,再利用等角直角三角形的性质及三角形内角和求出∠2的对顶角,即可求∠2.

解:如图,延BA,CD交于点E.
∵直尺为矩形,两组对边分别平行
∴∠1+∠4=180°,∠1=115°
∴∠4=180°-∠1=180°-115°=65°
∵∠EDA与∠4互为对顶角
∴∠EDA=∠4=65°
∵△EBC为等腰直角三角形
∴∠E=45°
∴在△EAD中,∠EAD=180°-∠E-∠EDA=180°-45°-65°=70°
∵∠2与∠EAD互为对顶角
∴∠2=∠EAD =70°
故选:B.
-
科目: 来源: 题型:
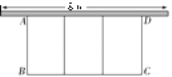
查看答案和解析>>【题目】如图,在一面靠墙的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
(1)求S与x的函数关系式及自变量的取值范围;
(2)已知墙的最大可用长度为8 m,
①求所围成花圃的最大面积;
②若所围花圃的面积不小于20 m2,请直接写出x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,某公园设计节日鲜花摆放方案,其中一个花坛由一批花盆堆成六角垛,顶层一个,以下各层堆成六边形,逐层每边增加一个花盆,若这垛花盆底层最长的一排共13个花盆,则底层的花盆的个数是( )
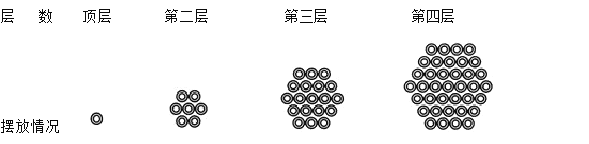
A.91B.127C.169D.255
-
科目: 来源: 题型:
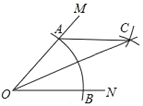
查看答案和解析>>【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】东方小商品市场一经营者将每件进价为80元的某种小商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种小商品单价每降低1元,其销量可增加10件.
(1)该经营者经营这种商品原来一天可获利润____元;
(2)若设后来该小商品每件降价x元,该经营者一天可获利润y元.
①若该经营者经营该商品一天要获利润2 090元,求每件商品应降价多少元?
②求出y与x之间的函数关系式,并求出当x取何值时,该经营者所获利润最大,且最大利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
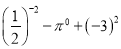 ;
;(2)
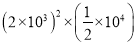 ;
;(3)2x3y(-2xy)+(-2x2y)2;
(4)(2a+b)(b-2a)-(a-3b)2.
-
科目: 来源: 题型:
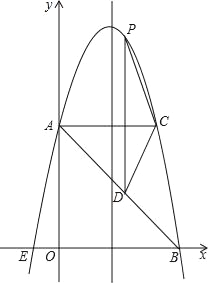
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
相关试题

