【题目】计算
(1)![]() ;
;
(2)![]() ;
;
(3)2x3y(-2xy)+(-2x2y)2;
(4)(2a+b)(b-2a)-(a-3b)2.
参考答案:
【答案】(1)12;(2)2×1010;(3)0;(4)-5a2+6ab-8b2.
【解析】
(1)先计算负整数指数幂、零指数幂和乘方,再计算加减可得;
(2)先计算积的乘方,再根据同底数的幂相乘即可得;
(3)先计算单项式乘单项式、单项式的乘方,再合并同类项即可得;
(4)先利用完全平方公式和平方差公式计算,再去括号、合并同类项即可得.
解:(1)原式=4-1+9=12;
(2)原式=4×106×![]() ×104=2×1010;
×104=2×1010;
(3)原式=-4x4y2+4x4y2=0;
(4)原式=b2-4a2-(a2-6ab+9b2)
=b2-4a2-a2+6ab-9b2
=-5a2+6ab-8b2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在∠MON中,以点O为圆心,任意长为半径作弧,交射线OM于点A,交射线ON于点B,再分别以A、B为圆心,OA的长为半径作弧,两弧在∠MON的内部交于点C,作射线OC,若OA=5,AB=6,则点B到AC的距离为_____.
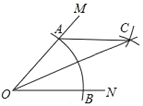
-
科目: 来源: 题型:
查看答案和解析>>【题目】一直尺与一缺了一角的等腰直角三角板如图摆放,若∠1=115°,则∠2的度数为( )
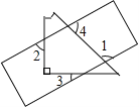
A.65°B.70°C.75°D.80°
-
科目: 来源: 题型:
查看答案和解析>>【题目】东方小商品市场一经营者将每件进价为80元的某种小商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种小商品单价每降低1元,其销量可增加10件.
(1)该经营者经营这种商品原来一天可获利润____元;
(2)若设后来该小商品每件降价x元,该经营者一天可获利润y元.
①若该经营者经营该商品一天要获利润2 090元,求每件商品应降价多少元?
②求出y与x之间的函数关系式,并求出当x取何值时,该经营者所获利润最大,且最大利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积.
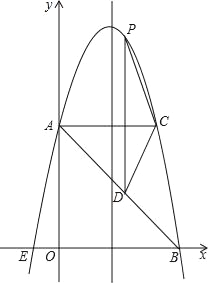
-
科目: 来源: 题型:
查看答案和解析>>【题目】若 x 满足 (9x)(x4)=4, 求 (4x)2+(x9)2 的值.
设 9x=a,x4=b, 则 (9x)(x4)=ab=4,a+b=(9x)+(x4)=5 ,
∴(9x)2+(x4)2=a2+b2=(a+b)22ab=522×4=13
请仿照上面的方法求解下面问题:
(1)若 x 满足 (5x)(x2)=2, 求 (5x)2+(x2)2 的值
(2)已知正方形 ABCD 的边长为 x , E , F 分别是 AD 、 DC 上的点,且 AE=1 , CF=3 ,长方形 EMFD 的面积是 48 ,分别以 MF 、 DF 作正方形,求阴影部分的面积.
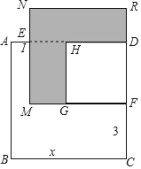
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

相关试题

