【题目】如图所示,在数轴上点A,B,C表示的数分别为﹣2,0,6.点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,点A与点C之间的距离表示为AC.
(1)AB= ,BC= ,AC= ;
(2)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时点B和点C分别以每秒2个单位长度和5个单位长度的速度向右运动.
①设运动时间为t,请用含有t的算式分别表示出AB,BC,AC;
②在①的条件下,请问:BC﹣AB的值是否随着运动时间t的变化而变化?若变化,请说明理由:若不变,请求其值.
![]()
参考答案:
【答案】(1)2,6,8;(2)①3t+2,3t+6,6t+8;②BC﹣AB的值不会随着运动时间t的变化而变化,其值为4
【解析】
(1)根据各个点在数轴上表示的数,求出AB、BC、AC的长,
(2)①用含有t的代数式表示出运动后,点A、B、C所表示的数,进而表示AB、BC、AC,
②根据BC、AB的长,计算BC﹣AB的值,得出结论.
解:(1)AB=|﹣2﹣0|=2,BC=|0﹣6|=6,AC=|﹣2﹣6|=8,
故答案为:2,6,8.
(2)①移动t秒后,点A所表示的数为(﹣2﹣t),点B所表示的数为2t,点C所表示的数为(6+5t),
因此,AB=2t﹣(﹣2﹣t)=3t+2,BC=(6+5t)﹣2t=3t+6,AC=6+5t﹣(﹣2﹣t)=6t+8,
②BC﹣AB=3t+6﹣(3t+2)=4,
答:BC﹣AB的值不会随着运动时间t的变化而变化,其值为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察与思考:阅读下列材料,并解决后面的问题
在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,过A作AD⊥BC于D(如图(1)),则
 ,即AD=csinB,AD=bsinC,于是csinB=bsinC,即
,即AD=csinB,AD=bsinC,于是csinB=bsinC,即 ,同理有:
,同理有:  ,所以
,所以 .
.即:在一个锐角三角形中,各边和它所对角的正弦的比相等在锐角三角形中,若已知三个元素(至少有一条边),运用上述结论和有关定理就可以求出其余三个未知元素.
根据上述材料,完成下列各题.

(1)如图(2),△ABC中,∠B=45°,∠C=75°,BC=60,则∠A= ;AC= ;
(2)某次巡逻中,如图(3),我渔政船在C处测得钓鱼岛A在我渔政船的北偏西30°的方向上,随后以40海里/时的速度按北偏东30°的方向航行,半小时后到达B处,此时又测得钓鱼岛A在的北偏西75°的方向上,求此时渔政船距钓鱼岛A的距离AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
(1)求点B的坐标;
(2)当点P在线段AB上运动(不与A,B重合)时,设点P的横坐标为m,线段CQ的长度为l.求出l关于m的函数解析式;
(3)在坐标平面内是否存在点D,使以O、P、Q、D为顶点的四边形为正方形?若存在,请直接写出D点的坐标;若不存在,请说明理由.
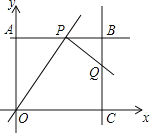
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,DC∥AB,AD=5,CD=3,sinA=sinB=
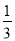 ,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )
,动点P自A点出发,沿着边AB向点B匀速运动,同时动点Q自点A出发,沿着边AD﹣DC﹣CB匀速运动,速度均为每秒1个单位,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(秒)时,△APQ的面积为s,则s关于t的函数图象是( )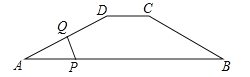
A.
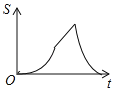 B.
B. 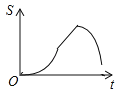
C.
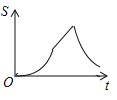 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】某景区的门票销售分两类:一类为散客门票,价格为
 元/张;另一类为团体门票(一次性购买门票
元/张;另一类为团体门票(一次性购买门票 张以上),每张门票价格在散客门票价格的基础上打
张以上),每张门票价格在散客门票价格的基础上打 折,某班部分同学要去该景点旅游,设参加旅游
折,某班部分同学要去该景点旅游,设参加旅游 人,购买门票需要
人,购买门票需要 元
元(1)如果每人分别买票,求
 与
与 之间的函数关系式:
之间的函数关系式:(2)如果购买团体票,求
 与
与 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;(3)请根据人数变化设计一种比较省钱的购票方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工分别住在A、B、C三个住宅区,A区有60人,B区有30人,C区有20人,三个区在同一条直线上,如图.该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )

A. A区 B. B区 C. C区 D. A、B两区之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的价目表如下(注:水费按月份结算,表示立方米)

请根据上表的内容解答下列问题:
(1)填空:若该户居民2月份用水5m3,则应交水费 元;3月份用水8m3,则应收水费 元;
(2)若该户居民4月份用水am3(其中a>10m3),则应交水费多少元(用含a的代数式表示,并化简)?
(3)若该户居民5、6两个月共用水14m3(6月份用水量超过了5月份),设5月份用水xm3,直接写出该户居民5、6两个月共交水费多少元(用含x的代数式表示).
相关试题

