搜索
【题目】当前正值草莓销售季节，小李用2000元在安塞区草莓基地购进草莓若干进行销售，由于销售状况良好，他又拿出6000元资金购进该种草莓，但这次的进货价比第一次的进货价提高了20%，购进草莓数量比第一次的2倍还多20千克。求该种草莓第一次进价是每千克多少元？
参考答案：
【答案】第一次进价是每千克50元
【解析】试题分析：设第一次进价是每千克x元，则第二次的进货价为x（1+20％）元，第一次购进草莓的数量为
千克，第二次购进草莓的数量为
千克，根据题意可列方程
=
×2+20，解出x即可.
试题解析：
设第一次进价是每千克x元，
=
×2+20，
6000=2000×1.2×2+20×1.2x，
x=50.
经检验，x=50不是方程的增根，所以此方程的解为x=50.
所以草莓第一次进价是每千克50元.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，AB＝AC，AD是△ABC的角平分线，点O为AB的中点，连接DO并延长到点E，使OE＝OD，连接AE，BE.
(1)求证：四边形AEBD是矩形；
(2)当△ABC满足什么条件时，矩形AEBD是正方形？并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某班组织班团活动，班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品，已知笔记本2元/本，中性笔1元/支，且每种奖品至少买1件．
（1）若设购买笔记本x本，中性笔y支，写出y与x之间的关系式；
（2）有多少种购买方案？请列举所有可能的结果；
（3）从上述方案中任选一种方案购买，求买到的中性笔与笔记本数量相等的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E．
（1）求证：AC平分∠DAB；
（2）连接BE交AC于点F，若cos∠CAD=
，求 
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在直角坐标系中，Rt△OAB的直角顶点A在x轴上，OA=4，AB=3．动点M从点A出发，以每秒1个单位长度的速度，沿AO向终点O移动；同时点N从点O出发，以每秒1.25个单位长度的速度，沿OB向终点B移动．当两个动点运动了x秒（0＜x＜4）时，解答下列问题：
（1）求点N的坐标（用含x的代数式表示）；
（2）设△OMN的面积是S，求S与x之间的函数表达式；当x为何值时，S有最大值？最大值是多少？
（3）在两个动点运动过程中，是否存在某一时刻，使△OMN是直角三角形？若存在，求出x的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，抛物线y=﹣
x2+mx+n的图象经过点A（2，3），对称轴为直线x=1，一次函数y=kx+b的图象经过点A，交x轴于点P，交抛物线于另一点B，点A、B位于点P的同侧．
（1）求抛物线的解析式；
（2）若PA：PB=3：1，求一次函数的解析式；
（3）在（2）的条件下，当k＞0时，抛物线的对称轴上是否存在点C，使得⊙C同时与x轴和直线AP都相切，如果存在，请求出点C的坐标，如果不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算:
(1)12+(-13)+8+(-7);
(2)
×
÷
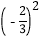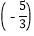;(3)-36×
;(4)-14-
÷
+[-2+(-2)2]-|2-4|.
相关试题
