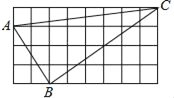
【题目】如图,正方形网格中有△ABC,若小方格边长为1,请你根据所学的知识解答下列问题:
(1)判断△ABC是什么形状?并说明理由.
(2)求△ABC中BC边上的高.
参考答案:
【答案】(1)△ABC是直角三角形.理由见解析;(2)![]()
【解析】
(1)根据勾股定理分别求出AB、BC、AC的长,再根据勾股定理的逆定理判断出三角形ABC的形状;
(2)设AC边上的高为h.根据△ABC的面积不变列出方程![]() ACh=
ACh=![]() ABBC,得出h=
ABBC,得出h=![]() ,代入数值计算即可.
,代入数值计算即可.
解:(1)△ABC是直角三角形.理由如下:
在Rt△ABC中,AB=![]() =
=![]() ;
;
在Rt△AEC中,AC=![]() ;
;
在Rt△BDC中,BC=![]() ;
;
∴AB2+BC2=AC2,
∴∠B=90°,△ABC是直角三角形;
(2)设AC边上的高为h.
∵S△ABC=![]() ACh=
ACh=![]() ABBC,
ABBC,
∴h=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A,B,C在同一直线上,线段AB=10cm且AC=6cm,M是AB的中点, N是AC的中点,则线段MN的长度是_________.
-
科目: 来源: 题型:
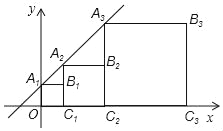
查看答案和解析>>【题目】如图,正方形A1B1C1D1、A2B2C2D2……按照如图所示的方式放置,点A1、A2、A3、…和点C1、C2、C3、…分别在直线y=kx+b(k>0)和x轴上,已知B1(1,1),B2(3,2),B3(7,4)则B2018的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在梯形ABCD中,AD∥BC,∠ABC=90°,AB=4,AD=8,sin∠BCD=
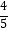 ,CE平分∠BCD,交边AD于点E,联结BE并延长,交CD的延长线于点P.
,CE平分∠BCD,交边AD于点E,联结BE并延长,交CD的延长线于点P. 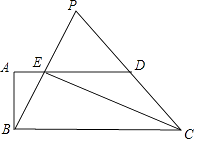
(1)求梯形ABCD的周长;
(2)求PE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是规格为8×8的正方形网格,请在所给的网格中按下列要求操作:
(1)请在网格中建立平面直角坐标系,使点A坐标为(﹣2,4),点B坐标为(﹣4,2);
(2)在第二象限内的格点上画一点C,使点C与线段AB组成一个以AB为底的等腰三角形,且腰长是无理数,则写出点C的坐标,写出△ABC的周长(结果保留根号);
(3)画出△ABC关于y轴的对称图形△A1B1C1;并写出点A1、B1、C1的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】文山州某中学为普遍提高学生身体素质,开展每天“阳光体育一小时”活动,根据实际情况决定开设A、篮球;B、乒乓球;C、羽毛球;D、足球四种运动项目,为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,每名学生必须且只能选择最喜爱的一项运动项目,并将调查结果制作成如下两幅不完整的统计图,请结合图中的信息解答下列问题:
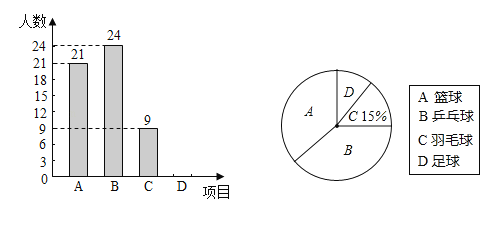
(1)这次被抽查的学生有人;请补全条形统计图;
(2)在统计图中,“乒乓球”对应扇形的圆心角是度;
(3)若该中学共有3600名学生,喜欢篮球的学生约有多少人?
相关试题

