【题目】甲乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)是一次函数关系,如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,每月在收取5500元的基础上,超过部分每平方米收取4元.

(1)求如图所示的y与x的函数解析式;(不要求写取值范围)
(2)如果某学校目前的绿化面积是1200平方米.试通过计算说明:选择哪家公司的服务,每月的绿化养护费用较少.
参考答案:
【答案】(1)y=5x+400.(2)选择乙公司的服务,每月的绿化养护费用较少.
【解析】试题分析:(1)利用待定系数法即可解决问题;
(2)绿化面积是1200平方米时,求出两家的费用即可判断;
试题解析:(1)设y=kx+b,则有![]() ,解得
,解得![]() ,
,
∴y=5x+400.
(2)绿化面积是1200平方米时,甲公司的费用为6400元,乙公司的费用为5500+4×200=6300元,
∵6300<6400
∴选择乙公司的服务,每月的绿化养护费用较少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是线段AB的垂直平分线,则∠CAD=∠CBD.请说明理由:

证明∵ CD是线段AB的垂直平分线(已知)
∴AC=BC, =BD
( ).
在△ACD和△BCD中,

∴△ACD≌△BCD(SSS ).
∴ ∠CAD=∠CBD( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式
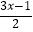 ﹣1≤
﹣1≤  ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来. -
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组:
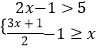 ,并在数轴上表示出不等式组的解集.
,并在数轴上表示出不等式组的解集. -
科目: 来源: 题型:
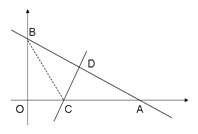
查看答案和解析>>【题目】如图:一次函数y=-
 x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.
x+6的图象与x轴和y轴分别交于点A和B ,再将△ AOB沿直线CD对折,使点A与点B重合。直线CD与x轴交于点C,与AB交于点D.(1)点A的坐标为 ,点B的坐标为 。
(2)求OC的长度 ;
(3)在x轴上有一点P,且△PAB是等腰三角形,不需计算过程,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】方程2x(x-1)=12+x(2x-5)的解是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式:3(x+2)>﹣1﹣2(x﹣1),并把解集在数轴上表示出来.
相关试题

