搜索
【题目】给出下列命题：其中，真命题的个数是（ ）
（1）平行四边形的对角线互相平分；（2）对角线相等的四边形是矩形；
（3）菱形的对角线互相垂直平分；（4）对角线互相垂直的四边形是菱形．
A.4B.3C.2D.1
参考答案：
【答案】C
【解析】
根据真命题的定义和特殊平行四边形的判定方法逐项分析可得结论.
解：（1）是平行四边形的性质，故（1）正确；
（2）对角线相等且互相平分的四边形是矩形；故（2）错误；
（3）是菱形的性质，故（3）正确；
（4）对角线互相垂直平分的四边形是菱形；故（4）错误；
因此正确的结论是（1）（3）；故选C．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（10分）如图，一次函数
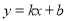与反比例函数
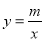的图象交于A（1，4），B（4，n）两点．
（1）求反比例函数的解析式；
（2）求一次函数的解析式；
（3）点P是x轴上的一动点，试确定点P并求出它的坐标，使PA+PB最小．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某地某日最高气温为12℃，最低气温为-7℃，该日气温的极差是 ℃．
-
科目： 来源： 题型：
查看答案和解析>>【题目】一个正方形花圃边长增加2m，所得新正方形花圃的周长是28m，设原正方形花圃的边长为xm，由此可得方程为（ ）
A. x+2=28 B. 4（x+2）=28 C. 2（x+2）=28 D. 4x+2=28
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，圆上有五个点，这五个点将圆分成五等份（每一份称为一段弧长），把这五个点按顺时针方向依次编号为1，2，3，4，5．若从某一点开始，沿圆周顺时针方向行走，点的编号是数字几，就走几段弧长，我们把这种走法称为一次“移位”．
如：小明在编号为3的点，那么他应走3段弧长，即从3→4→5→1为第1次“移位”，这时他到达编号为1的点，那么他应走1段弧长，即从1→2为第2次“移位”．
若小明从编号为4的点开始，第1次“移位”后，他到达编号为 的点，…，第2016次“移位”后，他到达编号为 的点．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∠CDE+∠CED=90°，EM平分∠CED，并与CD边交于点M．DN平分∠CED，并与EM交于点N．
（1）依题意补全图形，并猜想∠EDN+∠NED的度数等于 ；
（2）证明以上结论．
证明：∵DN平分∠CDE，EM平分∠CED，
∴∠EDN=
∠CDE，∠NED= ．（理由： ）
∵∠CDE+∠CED=90°，
∴∠EDN+∠NED= ×（∠ +∠ ）= ×90°= °．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1：在四边形ABCD中，AB＝AD，∠BAD＝120°，∠B＝∠ADC＝90°．E、F分别是BC、CD上的点．且∠EAF＝60°．探究图中线段BE、EF、FD之间的数量关系．
小王同学探究此问题的方法是，延长FD到点G，使DG＝BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是 ；
探索延伸：
如图2，若在四边形ABCD中，AB＝AD，∠B＋∠D＝180°．E、F分别是BC、CD上的点，且∠EAF＝
∠BAD，上述结论是否仍然成立，并说明理由；实际应用：
如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进1.5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离？
相关试题
