【题目】问题提出
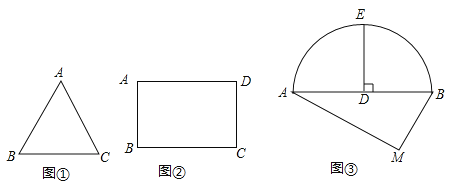
(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为 ;
问题探究
(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交![]() 于点E,又测得DE=8m.
于点E,又测得DE=8m.
请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
参考答案:
【答案】(1)![]() ;(2)PQ=
;(2)PQ=![]() ;(3)喷灌龙头的射程至少为19.71米.
;(3)喷灌龙头的射程至少为19.71米.
【解析】
试题分析:(1)构建Rt△AOD中,利用cos∠OAD=cos30°=![]() ,可得OA的长;
,可得OA的长;
(2)经过矩形对角线交点的直线将矩形面积平分,根据此结论作出PQ,利用勾股定理进行计算即可;
(3)如图3,作辅助线,先确定圆心和半径,根据勾股定理计算半径:
在Rt△AOD中,由勾股定理解得:r=13根据三角形面积计算高MN的长,证明△ADC∽△ANM,列比例式求DC的长,确定点O在△AMB内部,利用勾股定理计算OM,则最大距离FM的长可利用相加得出结论.
试题解析:(1)如图1,过O作OD⊥AC于D,则AD=![]() AC=
AC=![]() ×12=6,∵O是内心,△ABC是等边三角形,∴∠OAD=
×12=6,∵O是内心,△ABC是等边三角形,∴∠OAD=![]() ∠BAC=
∠BAC=![]() ×60°=30°,在Rt△AOD中,cos∠OAD=cos30°=
×60°=30°,在Rt△AOD中,cos∠OAD=cos30°=![]() ,∴OA=6÷
,∴OA=6÷![]() =
=![]() ,故答案为:
,故答案为:![]() ;
;
(2)存在,如图2,连接AC、BD交于点O,连接PO并延长交BC于Q,则线段PQ将矩形ABCD的面积平分,∵点O为矩形ABCD的对称中心,∴CQ=AP=3,过P作PM⊥BC于点,则PM=AB=12,MQ=18﹣3﹣3=12,由勾股定理得:PQ=![]() =
=![]() =
=![]() ;
;
(3)如图3,作射线ED交AM于点C.∵AD=DB,ED⊥AB,![]() 是劣弧,∴
是劣弧,∴![]() 所在圆的圆心在射线DC上,假设圆心为O,半径为r,连接OA,则OA=r,OD=r﹣8,AD=
所在圆的圆心在射线DC上,假设圆心为O,半径为r,连接OA,则OA=r,OD=r﹣8,AD=![]() AB=12,在Rt△AOD中,r2=122+(r﹣8)2,解得:r=13,∴OD=5,过点M作MN⊥AB,垂足为N,∵S△ABM=96,AB=24,∴
AB=12,在Rt△AOD中,r2=122+(r﹣8)2,解得:r=13,∴OD=5,过点M作MN⊥AB,垂足为N,∵S△ABM=96,AB=24,∴![]() ABMN=96,
ABMN=96,![]() ×24×MN=96,∴MN=8,NB=6,AN=18,∵CD∥MN,∴△ADC∽△ANM,∴
×24×MN=96,∴MN=8,NB=6,AN=18,∵CD∥MN,∴△ADC∽△ANM,∴![]() ,∴
,∴![]() ,
,![]() ,∴OD<CD,∴点O在△AMB内部,∴连接MO并延长交
,∴OD<CD,∴点O在△AMB内部,∴连接MO并延长交![]() 于点F,则MF为草坪上的点到M点的最大距离,∵在
于点F,则MF为草坪上的点到M点的最大距离,∵在![]() 上任取一点异于点F的点G,连接GO,GM,∴MF=OM+OF=OM+OG>MG,即MF>MG,过O作OH⊥MN,垂足为H,则OH=DN=6,MH=3,∴OM=
上任取一点异于点F的点G,连接GO,GM,∴MF=OM+OF=OM+OG>MG,即MF>MG,过O作OH⊥MN,垂足为H,则OH=DN=6,MH=3,∴OM=![]() =
=![]() =
=![]() ,∴MF=OM+r=
,∴MF=OM+r=![]() +13≈19.71(米).
+13≈19.71(米).
答:喷灌龙头的射程至少为19.71米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形有一个内角是120°,那么这个正多边形是正_____边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M是一个五次多项式,N是一个三次多项式,则M+N一定是( )
A. 五次多项式B. 五次整式C. 多项式D. 单项式
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知函数y=﹣
 x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.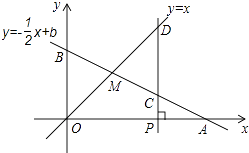
(1)求点A的坐标;
(2)在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣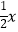 +b和y=x的图象于点C、D.
+b和y=x的图象于点C、D.
①若OB=2CD,求a的值;
②是否存在这样的点P,使以B、O、C、D为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
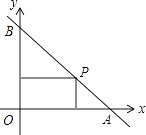
查看答案和解析>>【题目】如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
A.y=x+10
B.y=﹣x+10
C.y=x+20
D.y=﹣x+20 -
科目: 来源: 题型:
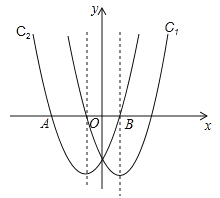
查看答案和解析>>【题目】在同一直角坐标系中,抛物线y=ax2﹣2x﹣3与抛物线y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解.
(1)ax2-2axy+ay2 (2)(2x+y)2﹣(x+2y)2
相关试题

