【题目】如图,已知函数y=﹣ ![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.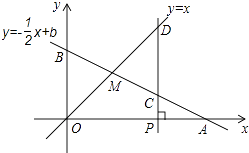
(1)求点A的坐标;
(2)在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ ![]() +b和y=x的图象于点C、D.
+b和y=x的图象于点C、D.
①若OB=2CD,求a的值;
②是否存在这样的点P,使以B、O、C、D为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵点M的横坐标为2,点M在直线y=x上,
∴M(2,2),
∵点M(2,2)在一次函数y=﹣ ![]() x+b的图象上,
x+b的图象上,
∴b=3,
∴一次函数的表达式为y=﹣ ![]() x+3,
x+3,
令y=0,得x=6,
∴点A的坐标为(6,0)
(2)解:①由题意得:C(a,﹣12a+3),D(a,a),
∴CD=a﹣(﹣ ![]() a+3)=
a+3)= ![]() a﹣3,
a﹣3,
∵OB=2CD.
∴2( ![]() a﹣3)=3,
a﹣3)=3,
∴a=3;
②存在,
∵CD∥OB,且以B、O、C、D为顶点的四边形是平行四边形,
∴OB=CD,
∴ ![]() a﹣3=3,解得a=4,
a﹣3=3,解得a=4,
∴P(4,0),
即存在满足条件的点P,其坐标为(4,0).
【解析】(1)可先求得M点坐标,代入直线y=﹣ ![]() x+b的解析式,令y=0则可求得A点坐标;(2)①用a可表示出C、D的坐标,从而可表示出CD的长,则由条件可得到关于a的方程,可求得a的值;②当四边形为平行四边形时则可得OB=CD,同①可得到关于a的方程,可求得a的值,则可求得P点坐标.
x+b的解析式,令y=0则可求得A点坐标;(2)①用a可表示出C、D的坐标,从而可表示出CD的长,则由条件可得到关于a的方程,可求得a的值;②当四边形为平行四边形时则可得OB=CD,同①可得到关于a的方程,可求得a的值,则可求得P点坐标.
【考点精析】利用平行四边形的判定对题目进行判断即可得到答案,需要熟知两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育课上,老师测量跳远成绩的依据是( )
A. 两点确定一条直线B. 两点之间,线段最短
C. 垂线段最短D. 平行线间的距离相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个正多边形有一个内角是120°,那么这个正多边形是正_____边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M是一个五次多项式,N是一个三次多项式,则M+N一定是( )
A. 五次多项式B. 五次整式C. 多项式D. 单项式
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题提出
(1)如图①,△ABC是等边三角形,AB=12,若点O是△ABC的内心,则OA的长为 ;
问题探究
(2)如图②,在矩形ABCD中,AB=12,AD=18,如果点P是AD边上一点,且AP=3,那么BC边上是否存在一点Q,使得线段PQ将矩形ABCD的面积平分?若存在,求出PQ的长;若不存在,请说明理由.
问题解决
(3)某城市街角有一草坪,草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成,如图③所示.管理员王师傅在M处的水管上安装了一喷灌龙头,以后,他想只用喷灌龙头来给这块草坪浇水,并且在用喷灌龙头浇水时,既要能确保草坪的每个角落都能浇上水,又能节约用水,于是,他让喷灌龙头的转角正好等于∠AMB(即每次喷灌时喷灌龙头由MA转到MB,然后再转回,这样往复喷灌.)同时,再合理设计好喷灌龙头喷水的射程就可以了.
如图③,已测出AB=24m,MB=10m,△AMB的面积为96m2;过弦AB的中点D作DE⊥AB交
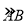 于点E,又测得DE=8m.
于点E,又测得DE=8m.请你根据以上信息,帮助王师傅计算喷灌龙头的射程至少多少米时,才能实现他的想法?为什么?(结果保留根号或精确到0.01米)
-
科目: 来源: 题型:
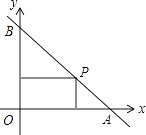
查看答案和解析>>【题目】如图,一直线与两坐标轴的正半轴分别交于A、B两点,P是线段AB上任意一点(不包括端点),过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20,则该直线的函数表达式是( )
A.y=x+10
B.y=﹣x+10
C.y=x+20
D.y=﹣x+20 -
科目: 来源: 题型:
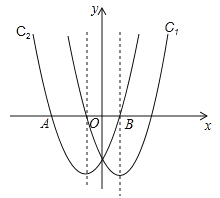
查看答案和解析>>【题目】在同一直角坐标系中,抛物线y=ax2﹣2x﹣3与抛物线y=x2+mx+n关于y轴对称,C2与x轴交于A、B两点,其中点A在点B的左侧.
(1)求抛物线C1,C2的函数表达式;
(2)求A、B两点的坐标;
(3)在抛物线C1上是否存在一点P,在抛物线C2上是否存在一点Q,使得以AB为边,且以A、B、P、Q四点为顶点的四边形是平行四边形?若存在,求出P、Q两点的坐标;若不存在,请说明理由.
相关试题

