搜索
【题目】因式分解.
(1)ax2-2axy+ay2 (2)（2x+y）2﹣（x+2y）2
参考答案：
【答案】（1）a(x-y）2； (2)3(x+y)(x-y).
【解析】
（1）先提取公因式a，再对余下的多项式利用完全平方公式继续分解；
（2）先提取公因式（x-y），再对余下的多项式利用平方差公式继续分解.
解：（1）ax2-2axy+ay2，
=a（x2-2xy+y2），
=a（x-y）2；
（2）（2x+y）2﹣（x+2y）2
=（2x+y+x+2y）（2x+y – x-2y），
=（3x+3y）（x-y）．
=3(x+y)(x-y)
-
科目： 来源： 题型：
查看答案和解析>>【题目】问题提出
（1）如图①，△ABC是等边三角形，AB=12，若点O是△ABC的内心，则OA的长为 ；
问题探究
（2）如图②，在矩形ABCD中，AB=12，AD=18，如果点P是AD边上一点，且AP=3，那么BC边上是否存在一点Q，使得线段PQ将矩形ABCD的面积平分？若存在，求出PQ的长；若不存在，请说明理由．
问题解决
（3）某城市街角有一草坪，草坪是由△ABM草地和弦AB与其所对的劣弧围成的草地组成，如图③所示．管理员王师傅在M处的水管上安装了一喷灌龙头，以后，他想只用喷灌龙头来给这块草坪浇水，并且在用喷灌龙头浇水时，既要能确保草坪的每个角落都能浇上水，又能节约用水，于是，他让喷灌龙头的转角正好等于∠AMB（即每次喷灌时喷灌龙头由MA转到MB，然后再转回，这样往复喷灌．）同时，再合理设计好喷灌龙头喷水的射程就可以了．
如图③，已测出AB=24m，MB=10m，△AMB的面积为96m2；过弦AB的中点D作DE⊥AB交
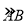于点E，又测得DE=8m．请你根据以上信息，帮助王师傅计算喷灌龙头的射程至少多少米时，才能实现他的想法？为什么？（结果保留根号或精确到0.01米）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，一直线与两坐标轴的正半轴分别交于A、B两点，P是线段AB上任意一点（不包括端点），过P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为20，则该直线的函数表达式是（ ）
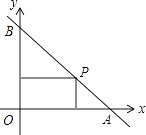
A.y=x+10
B.y=﹣x+10
C.y=x+20
D.y=﹣x+20 -
科目： 来源： 题型：
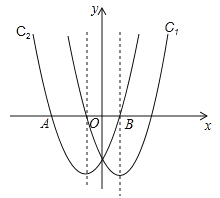
查看答案和解析>>【题目】在同一直角坐标系中，抛物线y=ax2﹣2x﹣3与抛物线y=x2+mx+n关于y轴对称，C2与x轴交于A、B两点，其中点A在点B的左侧．
（1）求抛物线C1，C2的函数表达式；
（2）求A、B两点的坐标；
（3）在抛物线C1上是否存在一点P，在抛物线C2上是否存在一点Q，使得以AB为边，且以A、B、P、Q四点为顶点的四边形是平行四边形？若存在，求出P、Q两点的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知一个等腰三角形一边长为3，周长为15，则它的腰长等于_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的边长为1，其面积标记为S1 ， 以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为S2 ， …，按照此规律继续下去，则S2017的值为（ ）
A.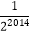
B.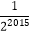
C.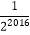
D.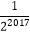
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，O为AC中点，过点O的直线分别与AB、CD交于点E、F，连结BF交AC于点M，连结DE、BO．若∠COB=60°，FO=FC，则下列结论：①FB垂直平分OC；②△EOB≌△CMB；③DE=EF；④S△AOE：S△BCM=2：3．其中正确结论的个数是（ ）
A.4个
B.3个
C.2个
D.1个
相关试题
