【题目】如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。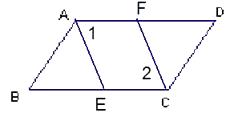
试说明:
(1)AE∥CF;
(2)AB∥CD。
参考答案:
【答案】
(1)解:∵AD∥CB (已知)
∴ ∠1=∠AEB (两直线平行,内错角相等)
又∵∠1=∠2(已知)
∴ ∠AEB= ∠2(等量代换)
∴AE∥CF(同位角相等,两直线平行)
(2)解:∵三角形ABE的内角和是180 ∴∠B+∠BAE+∠AEB=180
又∵∠AEB= ∠2(已证) ∠BAE=∠DCF(已知)
∴∠B+∠2+∠DCF=180 即∠B+∠BCD=180
∴AB∥CD(同旁内角互补,两直线平行)
【解析】(1)根据平行线的性质两直线平行,内错角相等得出∠1=∠AEB ,根据等量代换得出∠AEB= ∠2 ,根据平行线的判断同位角相等,两直线平行得出AE∥CF ;
(2)根据三角形的内角和得出∠B+∠BAE+∠AEB=180 ,又∠AEB= ∠2 , ∠BAE=∠DCF ,利用等量代换得出∠B+∠2+∠DCF=180 , 即∠B+∠BCD=180 ,根据平行线的判断同旁内角互补,两直线平行得出AB∥CD 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面内,直线a、b相交于O,b∥c,则a与c的位置关系是( )
A.平行
B.相交
C.重合
D.平行或重合 -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(x+2)(x-2)+(3x-1)(3x+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( )
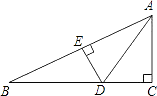
A.3 cm
B.4 cm
C.5 cm
D.不能确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例.
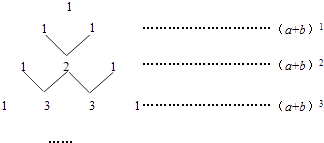
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
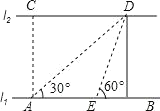
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
相关试题

