【题目】如图,在△ABC中,∠C=90°,AC=4cm,AB=7cm,AD平分∠BAC交BC于点D,DE⊥AB于点E,则EB的长是( ) 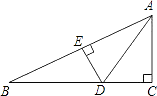
A.3 cm
B.4 cm
C.5 cm
D.不能确定
参考答案:
【答案】A
【解析】解:∵AD平分∠BAC交BC于点D,DE⊥AB,∠C=90°,
∴DE=DC,
在Rt△AED和Rt△ACD中,
∵AD=AD,DE=DC,
∴Rt△AED≌Rt△ACD(HL),
∴AE=AC=4cm,
∴BE=AB﹣AE=3cm,
故选:A.
【考点精析】根据题目的已知条件,利用角平分线的性质定理和勾股定理的概念的相关知识可以得到问题的答案,需要掌握定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读以下两小题后作出相应的解答:
(1)“同位角相等,两直线平行”,“两直线平行,同位角相等”,这两个命题的题设和结论在命题中的位置恰好对凋,我们把其中一命题叫做另一个命题的逆命题,请你写出命题“角平分线上的点到角两边的距离相等“的逆命题,并指出逆命题的题设和结论;
(2)根据以下语句作出图形,并写出该命题的文字叙述.
已知:过直线AB上一点O任作射线OC,OM、ON分别平分∠AOC、∠BOC,则OM⊥ON. -
科目: 来源: 题型:
查看答案和解析>>【题目】化简:(x+2)(x-2)+(3x-1)(3x+1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD∥CB,∠1=∠2,∠BAE=∠DCF。
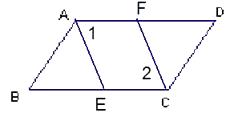
试说明:
(1)AE∥CF;
(2)AB∥CD。 -
科目: 来源: 题型:
查看答案和解析>>【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例.
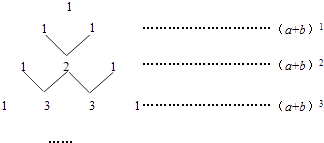
这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+ab+b2展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b3展开式中各项的系数等等.根据上面的规律,(a+b)4的展开式中各项系数最大的数为( )
A.4
B.5
C.6
D.7 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,河的两岸l1与l2相互平行,A、B是l1上的两点,C、D是l2上的两点,某人在点A处测得∠CAB=90°,∠DAB=30°,再沿AB方向前进20米到达点E(点E在线段AB上),测得∠DEB=60°,求C、D两点间的距离.
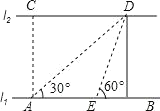
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列五个命题:①直径是弦,②优弧大于劣弧,③等弧的弧长相等,④平分弦的直径垂直于弦,⑤等弧所对的弦相等.其中正确的有( )个.
A.2B.3C.4D.5
相关试题

