【题目】对于任意两个实数对(a,b)和(c,d),规定:当且仅当a=c且b=d时, (a,b)=(c,d).定义运算“![]() ”:(a,b)
”:(a,b)![]() (c,d)=(ac-bd,ad+bc).若(1,2)
(c,d)=(ac-bd,ad+bc).若(1,2)![]() (p,3)=(q,q),则pq=___________.
(p,3)=(q,q),则pq=___________.
参考答案:
【答案】135
【解析】
首先根据运算“⊕”:(a,b)⊕(c,d)=(ac-bd,ad+bc),可知(1,2)⊕(p,3)=(p-6,3+2p),再由规定:当且仅当a=c且b=d时,(a,b)=(c,d),得出p-6=q,3+2p=q,解出p,q的值,即可得出结果.
根据题意可知(1,2)![]() (p,3)=(p-6,3+2p)=(q,q),
(p,3)=(p-6,3+2p)=(q,q),
∴p-6=q,3+2p=q,
解得p=-9,q=-15,
Pq=(-9)×(-15)=135.
故答案为:135.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;……;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,……,则线段D1D2的长为______,线段Dn-1Dn的长为______(n为正整数).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这
个分式为“和谐分式”.
(1)下列分式:①
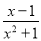 ;②
;②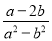 ;③
;③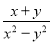 ;④
;④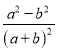 . 其中是“和谐分式”是 (填写序号即可);
. 其中是“和谐分式”是 (填写序号即可);(2)若
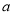 为正整数,且
为正整数,且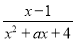 为“和谐分式”,请写出
为“和谐分式”,请写出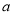 的值;
的值;(3)在化简
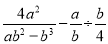 时,
时,小东和小强分别进行了如下三步变形:
小东:
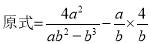
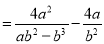
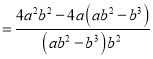
小强:
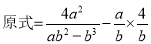
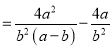
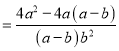
显然,小强利用了其中的和谐分式, 第三步所得结果比小东的结果简单,
原因是: ,
请你接着小强的方法完成化简.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学要证明命题“平行四边形的对边相等.”是正确的,他画出了图形,并写出了如下已知和不完整的求证.
已知:如图,四边形ABCD是平行四边形.
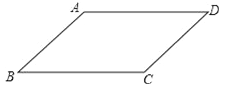
求证:AB=CD,
(1)补全求证部分;
(2)请你写出证明过程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)5
 -3
-3 +4
+4 -
-
(2)(
 -
- -
-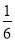 )×(-36)
)×(-36)(3)-
 ―(1―0.5)÷
―(1―0.5)÷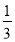 ×[2+(-4)2]
×[2+(-4)2] (4)(
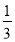 -
- )×52÷|-
)×52÷|-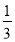 |+(
|+( )2019×42020
)2019×42020 -
科目: 来源: 题型:
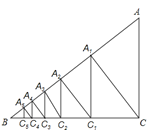
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠ACB=90°,AC=6,BC=8,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直作下去,得到了一组线段CA1,A1C1,C1A2,A2C2,…,AnCn,则A1C1=_________,AnCn=__________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干个奇数按每行8个数排成如图的形式:
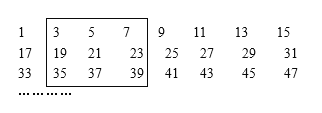
小军画了一方框框住了其中的9个数.
(1)如图中方框内9个数之和是 ;
(2)若小军画的方框内9个数之和等于333,则这个方框内左下角的那个数为_________;
(3)试说明:方框内的9个数之和总是9的倍数.
相关试题

