Question

【题目】如图，已知抛物线y=ax2+bx+4与x轴交于A（﹣2，0）、B两点，与y轴交于C点，其对称轴为直线x=1．

（1）直接写出抛物线的解析式： ；

（2）把线段AC沿x轴向右平移，设平移后A、C的对应点分别为A′、C′，当C′落在抛物线上时，求A′、C′的坐标；

（3）除（2）中的点A′、C′外，在x轴和抛物线上是否还分别存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形？若存在，求出E、F的坐标；若不存在，请说明理由．

Answer 1

【答案】（1）y=﹣x2+x+4；（2）C′（2，4），A′（0，0）．（3）见解析

【解析】

试题分析：（1）先求得B点的坐标，然后根据待定系数法交点抛物线的解析式；

（2）根据平移性质及抛物线的对称性，求出A′、C′的坐标；

（3）以A、C、E、F为顶点的四边形为平行四边形，可能存在3种满足条件的情形，需要分类讨论，避免漏解．

解：（1）∵A（﹣2，0），对称轴为直线x=1．

∴B（4，0），

把A（﹣2，0），B（4，0）代入抛物线的表达式为：

，

解得：，

∴抛物线的解析式为：y=﹣x2+x+4；

（2）由抛物线y=﹣x2+x+4可知C（0，4），

∵抛物线的对称轴为直线x=1，根据对称性，

∴C′（2，4），

∴A′（0，0）．

（3）存在．

设F（x，﹣x2+x+4）．

以A、C、E、F为顶点的四边形为平行四边形，

①若AC为平行四边形的边，如答图1﹣1所示，则EF∥AC且EF=AC．

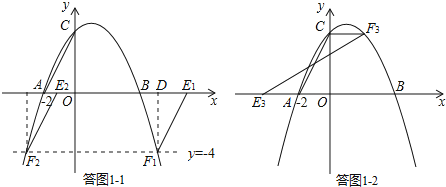
过点F1作F1D⊥x轴于点D，则易证Rt△AOC≌Rt△E1DF1，

∴DE1=2，DF1=4．

∴﹣x2+x+4=﹣4，

解得：x1=1+，x2=1﹣．

∴F1（1+，﹣4），F2（1﹣，﹣4）；

∴E1（3+，0），E2（3﹣，0）．

②若AC为平行四边形的对角线，如答图1﹣2所示．

∵点E3在x轴上，∴CF3∥x轴，

∴点C为点A关于x=1的对称点，

∴F3（2，4），CF3=2．

∴AE3=2，

∴E3（﹣4，0），

综上所述，存在点E、F，使得以A、C、E、F为顶点的四边形为平行四边形；

点E、F的坐标为：E1（3+，0），F1（1+，﹣4）；E2（3﹣，0），F2（1﹣，﹣4）；E3（﹣4，0），F3（2，4）．