【题目】如图,在△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠BAC=50°,∠C=70°,求∠DAC和∠BOA的度数

参考答案:
【答案】∠DAC=20°;∠BOA=125°.
【解析】
因为AD是高,所以∠ADC=90°,又因为∠C=70°,所以∠DAC度数可求;因为∠BAC=50°,∠C=70°,所以∠BAO=25°,∠ABC=60°,BF是∠ABC的角平分线,则∠ABO=30°,故∠BOA的度数可求.
∵AD⊥BC
∴∠ADC=90°
∵∠C=70°
∴∠DAC=180°-90°-70°=20°;
∵∠BAC=50°,∠C=70°
∴∠BAO=25°,∠ABC=60°
∵BF是∠ABC的角平分线
∴∠ABO=30°
∴∠BOA=180°-∠BAO-∠ABO=180°-25°-30°=125°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知P(3,3),点B、A分别在x轴正半轴和y轴正半轴上,∠APB=90°,则OA+OB=________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图.在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折,B点落在D点的位置,且AD交y轴于点E.那么点D的坐标为( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点E,F,G分别是等边三角形ABC三边AB,BC,CA上的动点,且始终保持AE=BF=CG,设△EFG的面积为y,AE的长为x,y关于x的函数图象大致为图2所示,则等边三角形ABC的边长为___.

-
科目: 来源: 题型:
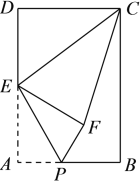
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=6,点E为AD的中点,点P为线段AB上一个动点,连接EP,将△APE沿EP折叠得到△EPF,连接CE,CF,当△ECF为直角三角形时,AP的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠BAC=36°,AD平分∠BAC,AM⊥AD交BC的延长线于M,若BM=BA+AC,则∠ABC=_________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解学生的体能状况,某学校从七年级学生中随机抽取部分学生的体能测试结果进行分析,并根据收集的数据绘制了两幅不完整的统计图,请根据这两幅统计图中的信息回答下列问题:(测试结果分“优秀”、“良好”、“及格”、“不及格”四个等级)
(1)本次抽样调查共抽取多少名学生?
(2)补全条形统计图.
(3)在扇形统计图中,求测试结果为“良好”等级所对应圆心角的度数.
(4)若该学校七年级共有600名学生,请你估计该学校七年级学生中测试结果为“不及格”等级的学生有多少名?

相关试题

