搜索
【题目】一条抛物线的开口大小与方向、对称轴均与抛物线y=
x2相同，并且抛物线经过点(1，1)．
（1）求抛物线的解析式，并指明其顶点；
（2）所求抛物线如何由抛物线y=x2平移得到？
参考答案：
【答案】（1）y=
x2+，其顶点是(0，)；（2）抛物线y=x2向上平移个单位可得所求抛物线y=x2+．
【解析】
（1）根据二次函数的开口方向和大小、对称轴相同设出其解析式为y=x2+k，利用待定系数法求出解析式，然后判断出顶点坐标；
（2）根据二次函数的平移规律：上加下减，左加右减，判断即可.
（1）根据题意，可设所求抛物线的解析式为y=x2+k，把点(1，1)代入上式，得×12+k=1，解得k=．所以抛物线的解析式为y=x2+，其顶点是(0，)．
（2）抛物线y=x2向上平移个单位可得所求抛物线y=x2+．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28 m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=x m．若在P处有一棵树与墙CD，AD的距离分别是15 m和6 m，要将这棵树围在花园内（含边界，不考虑树的粗细），则花园面积S的最大值为（ ）
A. 196 B. 195 C. 132 D. 14
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在长方形
中，
，有一只蚂蚁
在点
处开始以每秒1个单位的速度沿
边向点
爬行，另一只蚂蚁
从点以每秒2个单位的速度沿
边向点
爬行，蚂蚁的大小忽略不计，如果、同时出发，设运动时间为
s.
(1)当
时，求
的面积; (2)当
时，试说明
是直角二角形;(3)当运动3s时，
点停止运动，点以原速立即向点返回，在返回的过程中，是否存在点，使得
平分
?若存在，求出点运动的时间，若不存在请说明理由. -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，二次函数y=－x2+2x+m的图象与x轴的一个交点为A(3，0)，另一个交点为B，且与y轴交于点C．若该二次函数图象上有一点D(x，y)，使S△ABD=S△ABC，则D点的坐标为____________________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知点A（0，2），B（2，2），C（-1，-2），抛物线F：y=x2-2mx+m2-2与直线x=-2交于点P．
（1）当抛物线F经过点C时，求它的解析式；
（2）设点P的纵坐标为yP，求yP的最小值，此时抛物线F上有两点（x1，y1），（x2，y2），且x1＜x2≤-2，比较y1与y2的大小.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠A＝90°，∠C＝30°，AD⊥BC于D，BE是∠ABC的平分线，且交AD于P，如果AP＝2，则P点到AB的距离为( )
A.1B.2C.3D.4
-
科目： 来源： 题型：
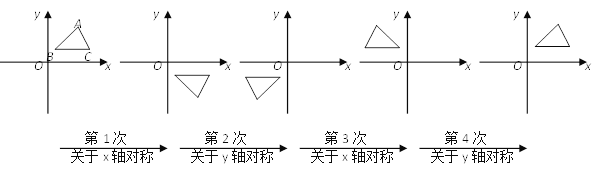
查看答案和解析>>【题目】如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是（2，3），则经过第2018次变换后所得的A点坐标是________．
相关试题
