【题目】如图,已知点A(0,2),B(2,2),C(-1,-2),抛物线F:y=x2-2mx+m2-2与直线x=-2交于点P.
(1)当抛物线F经过点C时,求它的解析式;
(2)设点P的纵坐标为yP,求yP的最小值,此时抛物线F上有两点(x1,y1),(x2,y2),且x1<x2≤-2,比较y1与y2的大小.

参考答案:
【答案】(1) ![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据抛物线F:y=x2-2mx+m2-2过点C(-1,-2),可以求得抛物线F的表达式;
(2)根据题意,可以求得yP的最小值和此时抛物线的表达式,从而可以比较y1与y2的大小.
(1) ∵抛物线F经过点C(-1,-2),
∴![]() .
.
∴m1=m2=-1.
∴抛物线F的解析式是![]() .
.
(2)当x=-2时,![]() =
=![]() .
.
∴当m=-2时,![]() 的最小值为-2.
的最小值为-2.
此时抛物线F的表达式是![]() .
.
∴当![]() 时,y随x的增大而减小.
时,y随x的增大而减小.
∵![]() ≤-2,
≤-2,
∴![]() >
>![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在长方形
 中,
中, ,有一只蚂蚁
,有一只蚂蚁 在点
在点 处开始以每秒1个单位的速度沿
处开始以每秒1个单位的速度沿 边向点
边向点 爬行,另一只蚂蚁
爬行,另一只蚂蚁 从点
从点 以每秒2个单位的速度沿
以每秒2个单位的速度沿 边向点
边向点 爬行,蚂蚁的大小忽略不计,如果
爬行,蚂蚁的大小忽略不计,如果 、
、 同时出发,设运动时间为
同时出发,设运动时间为 s.
s.
(1)当
 时,求
时,求 的面积;
的面积; (2)当
 时,试说明
时,试说明 是直角二角形;
是直角二角形;(3)当运动3s时,
 点停止运动,
点停止运动, 点以原速立即向
点以原速立即向 点返回,在返回的过程中,是否存在点
点返回,在返回的过程中,是否存在点 ,使得
,使得 平分
平分 ?若存在,求出点
?若存在,求出点 运动的时间,若不存在请说明理由.
运动的时间,若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=-x2+2x+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.若该二次函数图象上有一点D(x,y),使S△ABD=S△ABC,则D点的坐标为____________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一条抛物线的开口大小与方向、对称轴均与抛物线y=
 x2相同,并且抛物线经过点(1,1).
x2相同,并且抛物线经过点(1,1).(1)求抛物线的解析式,并指明其顶点;
(2)所求抛物线如何由抛物线y=
 x2平移得到?
x2平移得到? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠A=90°,∠C=30°,AD⊥BC于D,BE是∠ABC的平分线,且交AD于P,如果AP=2,则P点到AB的距离为( )

A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,对△ABC进行循环往复的轴对称变换,若原来点A坐标是(2,3),则经过第2018次变换后所得的A点坐标是________.
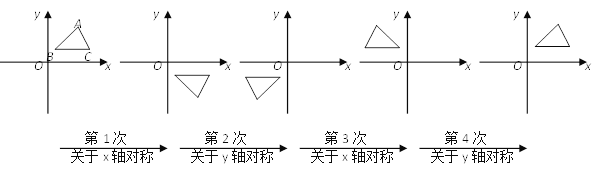
-
科目: 来源: 题型:
查看答案和解析>>【题目】(12分)如图所示是隧道的截面由抛物线和长方形构成,长方形的长是12 m,宽是4 m.按照图中所示的直角坐标系,抛物线可以用y=
 x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为
x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m.
m. (1)求抛物线的函数关系式,并计算出拱顶D到地面OA的距离;
(2)一辆货运汽车载一长方体集装箱后高为6m,宽为4m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在抛物线型拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8m,那么两排灯的水平距离最小是多少米?

相关试题

