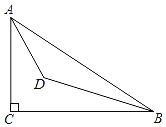
【题目】如图,∠C=90°,AC=3,BC=4,∠ABC和∠BAC的角平分线的交点是点D,则△ABD的面积为_____.
参考答案:
【答案】2.5.
【解析】
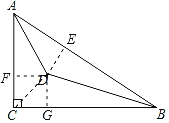
连接CD,过D作DE⊥AB于E,DF⊥AC于F, DG⊥BC于G,根据勾股定理求出AB,根据角平分线的性质得到DE=DF=DG,根据三角形的面积公式计算,得到答案.
解:连接CD,作DE⊥AB于E,DF⊥AC于F,DG⊥BC于G,
由勾股定理得,![]()
∵点D是∠ABC和∠BAC的角平分线的交点,DE⊥AB,DF⊥AC,DG⊥BC,
∴DE=DF=DG,
∵![]() ×AB×DE+
×AB×DE+![]() ×AC×DF+
×AC×DF+![]() ×BC×DG=
×BC×DG=![]() ×AC×BC,
×AC×BC,
即![]() ×5×DE+
×5×DE+![]() ×3×DF+
×3×DF+![]() ×4×DG=
×4×DG=![]() ×3×4,
×3×4,
解得:DE=1,
∴△ABD的面积为:![]() ×5×1=2.5,
×5×1=2.5,
故答案为:2.5.
-
科目: 来源: 题型:
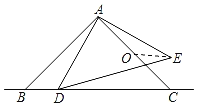
查看答案和解析>>【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=2,O为AC中点,若点D在直线BC上运动,连接OE,则在点D运动过程中,则OE的最小值是为( )
A.
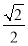 B.0.25C.1D.2
B.0.25C.1D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某开发区有一块四边形的空地ABCD,现计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,则要投入_____元.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2+ax+a-2=0.
(1)求证:不论a取何实数,该方程都有两个不相等的实数根;
(2)若该方程的一个根为1,求a的值及该方程的另一根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.
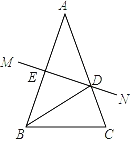
(1)若∠A=40°,求∠DBC的度数;
(2)若AE=6,△CBD的周长为20,求△ABC的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D与点B重合,点C落在点C′的位置上.
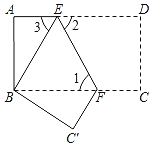
(1)折叠后,DC的对应线段是 ,CF的对应线段是 .
(2)若∠1=55°,求∠2、∠3的度数;
(3)若AB=6,AD=12,求△BC′F的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AD∥BC

 ,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.
,点E是边AD的中点,连接BE交AC于F,BE的延长线交CD的延长线于G.(1)求证:
 ;
;(2)若GE=2,BF=3,求线段EF的长.

相关试题

