【题目】如图,四边形ABCD中,E,F,G,H依次是各边中点,O是四边形内一点,若S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,则S四边形DHOG= . 
参考答案:
【答案】4
【解析】解:连接OC,OB,OA,OD, 
∵E、F、G、H依次是各边中点,
∴△AOE和△BOE等底等高,所以S△OAE=S△OBE ,
同理可证,S△OBF=S△OCF , S△ODG=S△OCG , S△ODH=S△OAH ,
∴S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE ,
∵S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,
∴3+5=4+S四边形DHOG ,
解得,S四边形DHOG=4.
故应填4.
连接OC,OB,OA,OD,易证S△OBF=S△OCF , S△ODG=S△OCG , S△ODH=S△OAH , S△OAE=S△OBE , 所以S四边形AEOH+S四边形CGOF=S四边形DHOG+S四边形BFOE , 所以可以求出S四边形DHOG .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(a2﹣b2)﹣4(2a2﹣3b2)
(2)3x2+[2x﹣(﹣5x2+2x)﹣2]﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中∠A=30°,E是AC边上的点,先将△ABE沿着BE翻折,翻折后△ABE的AB边交AC于点D,又将△BCD沿着BD翻折,C点恰好落在BE上,此时∠CDB=82°,则原三角形的∠B为( )

A.75°
B.76°
C.77°
D.78° -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,已知∠ABC=50°,∠ACB=60°,BE是AC上的高,CF是AB上的高,H是BE和CF的交点,则 ∠BHC= .
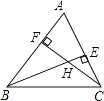
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=4x2﹣3y2﹣6xy,B=3xy﹣2y2﹣x2 , 当x=2,y=﹣3时,求2A﹣3B的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知13.5亿是由四舍五入取得的近似数,它精确到( )
A.十分位
B.千万位
C.亿位
D.十亿位 -
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB=2
 ,P是AC上的一个动点.
,P是AC上的一个动点.
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时□DPBQ的面积.
相关试题

