【题目】如图1,MA1∥NA2 , 则∠A1+∠A2= 度.
如图2,MA1∥NA3 , 则∠A1+∠A2+∠A3= 度.
如图3,MA1∥NA4 , 则∠A1+∠A2+∠A3+∠A4= 度.
如图4,MA1∥NA5 , 则∠A1+∠A2+∠A3+∠A4+∠A5= 度.从上述结论中你发现了什么规律?
如图5,MA1∥NAn , 则∠A1+∠A2+∠A3+…+∠An= 度.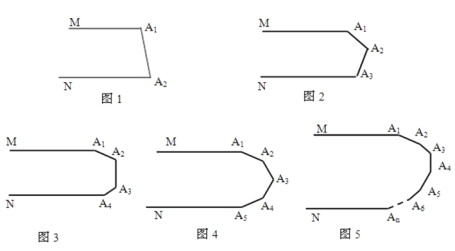
参考答案:
【答案】180;360;540;720;180(n﹣1)
【解析】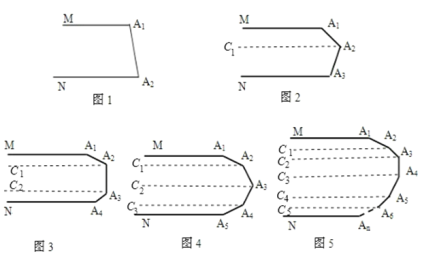
解:如图1,
∵MA1∥NA2 ,
∴∠A1+∠A2=180°.
如图2,过点A2作A2C1∥A1M,
∵MA1∥NA3 ,
∴A2C1∥A1M∥NA3 ,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A3=180°,
∴∠A1+∠A2+∠A3=360°.
如图3,过点A2作A2C1∥A1M,过点A3作A3C2∥A1M,
∵MA1∥NA3 ,
∴A2C1∥A3C2∥A1M∥NA3 ,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A2A3C2=180°,∠C2A3A4+∠A4=180°,
∴∠A1+∠A2+∠A3+∠A4=540°.
如图4,过点A2作A2C1∥A1M,过点A3作A3C2∥A1M,过点A4作A4C3∥A1M,
∵MA1∥NA5 ,
∴A2C1∥A3C2∥A4C3∥NA5 ,
∴∠A1+∠A1A2C1=180°,∠C1A2A3+∠A2A3C2=180°,∠C2A3A4+∠A3A4C3=180°∠C3A4A5+∠A5=180°,
∴∠A1+∠A2+∠A3+∠A4+∠A5=720°.
从上述结论中你发现了规律:如图5,MA1∥NAn , 则∠A1+∠A2+∠A3+…+∠An=180(n﹣1)度.
所以答案是:180,360,540,720,180(n﹣1).
【考点精析】通过灵活运用平行线的性质,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.矩形的对角线互相垂直B.菱形的对角线相等
C.正方形的对角线互相垂直平分且相等D.平行四边形的对角线平分一组对角
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1,x2是一元二次方程x2+2x-4=0的两个实数根,则x12+3x1+x2+x1x2=__.
-
科目: 来源: 题型:
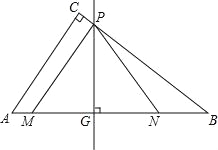
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
(1)当t= 秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式.
-
科目: 来源: 题型:
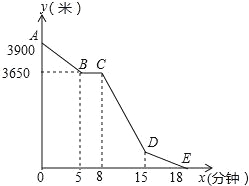
查看答案和解析>>【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)小丽步行的速度为 ;
(2)写出y与x之间的函数关系式: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式6a3﹣54a分解因式的结果为__.
-
科目: 来源: 题型:
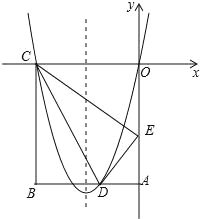
查看答案和解析>>【题目】如图,在矩形OABC中,OA=5,AB=4,点D为边AB上一点,将△BCD沿直线CD折叠,使点B恰好落在边OA上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系.
(1)求OE的长及经过O,D,C三点抛物线的解析式;
(2)一动点P从点C出发,沿CB以每秒2个单位长度的速度向点B运动,同时动点Q从E点出发,沿EC以每秒1个单位长度的速度向点C运动,当点P到达点B时,两点同时停止运动,设运动时间为t秒,当t为何值时,DP=DQ;
(3)若点N在(1)中抛物线的对称轴上,点M在抛物线上,是否存在这样的点M与点N,使M,N,C,E为顶点的四边形是平行四边形?若存在,请求出M点坐标;若不存在,请说明理由.
相关试题

