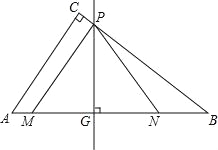
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
(1)当t= 秒时,动点M、N相遇;
(2)设△PMN的面积为S,求S与t之间的函数关系式.
参考答案:
【答案】(1)2.5
(2)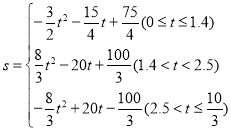
【解析】
试题分析:(1)根据勾股定理可得AB=10,若动点M、N相遇,则有t+3t=10,即可求出t的值;
(2)由于“点P在BC上”与“点P在点AC上”及“点M在点N的左边”与“点M在点N的右边”对应的MN、PG的表达式不同,S与t之间的函数关系式也就不同,因此需分情况讨论.只需先考虑临界位置(点P与点C重合,点M与点N重合、点N与点A重合)所对应的t的值,然后分三种情况(①0≤t≤1.4,②1.4<t<2.5,③2.5<t≤![]() )讨论,用t的代数式表示出MN和PG,就可解决问题.
)讨论,用t的代数式表示出MN和PG,就可解决问题.
试题解析:(1)∵∠ACB=90°,AC=6,BC=8,∴AB=10,
∴t+3t=10,解得t=2.5(s),
即当t=2.5秒时,动点M,N相遇;
故答案为2.5;
(2)过点C作CH⊥AB于H,
由S△ABC=![]() ACBC=
ACBC=![]() ABCH得,CH=
ABCH得,CH=![]() =4.8,
=4.8,
∴AH=![]() =3.6,BH=10﹣3.6=6.4.
=3.6,BH=10﹣3.6=6.4.
∵当点N运动到点A时,M,N两点同时停止运动,∴0≤t≤![]() .
.
当0≤t<2.5时,点M在点N的左边,如图1、图2,
MN=AB﹣AM﹣BN=10﹣t﹣3t=10﹣4t.
∵点G是MN的中点,∴MG=![]() MN=5﹣2t,
MN=5﹣2t,
∴AG=AM+MG=t+5﹣2t=5﹣t,
∴BG=10﹣(5﹣t)=t+5.
当点P与点C重合时,点G与点H重合,
则有5﹣t=3.6,解得t=1.4.
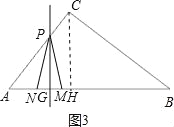
当2.5<t≤![]() 时,点M在点N右边,如图3,
时,点M在点N右边,如图3,
∵MN=AM﹣AN=AM﹣(AB﹣BN)=t﹣(10﹣3t)=4t﹣10,
∴NG=![]() MN=2t﹣5,
MN=2t﹣5,
∴AG=AN+NG=10﹣3t+2t﹣5=5﹣t.
综上所述:①当0≤t≤1.4时,点M在点N的左边,点P在BC上,如图1,
此时MN=10﹣4t,BG=t+5,PG=BGtanB=![]() (t+5)=
(t+5)=![]() t+
t+![]() ,
,
∴S=![]() MNPG=
MNPG=![]() (10﹣4t)(
(10﹣4t)(![]() t+
t+![]() )=﹣
)=﹣![]() t2﹣
t2﹣![]() t+
t+![]() ;
;
②当1.4<t<2.5时,点M在点N的左边,点P在AC上,如图2,
此时MN=10﹣4t,AG=5﹣t,PG=AGtanA=![]() (5﹣t)=
(5﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=![]() MNPG=
MNPG=![]() (10﹣4t)(
(10﹣4t)(![]() ﹣
﹣![]() t)=
t)=![]() t2﹣20t+
t2﹣20t+![]() ;
;
③当2.5<t≤![]() 时,点M在点N的右边,点P在AC上,如图3,
时,点M在点N的右边,点P在AC上,如图3,
此时MN=4t﹣10,AG=5﹣t,PG=AGtanA=![]() (5﹣t)=
(5﹣t)=![]() ﹣
﹣![]() t,
t,
∴S=![]() MNPG=
MNPG=![]() (4t﹣10)(
(4t﹣10)(![]() ﹣
﹣![]() t)=﹣
t)=﹣![]() t2+20t﹣
t2+20t﹣![]() ;
;
∴S与t之间的函数关系式为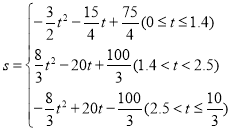 .
.


-
科目: 来源: 题型:
查看答案和解析>>【题目】下列结论正确的是 ( )
A.两数之积为正,这两数同为正
B.两数之积为负,这两数为异号
C.几个数相乘,积的符号由负因数的个数决定
D.三数相乘,积为负,这三个数都是负数 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,真命题是( )
A.矩形的对角线互相垂直B.菱形的对角线相等
C.正方形的对角线互相垂直平分且相等D.平行四边形的对角线平分一组对角
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x1,x2是一元二次方程x2+2x-4=0的两个实数根,则x12+3x1+x2+x1x2=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,MA1∥NA2 , 则∠A1+∠A2= 度.
如图2,MA1∥NA3 , 则∠A1+∠A2+∠A3= 度.
如图3,MA1∥NA4 , 则∠A1+∠A2+∠A3+∠A4= 度.
如图4,MA1∥NA5 , 则∠A1+∠A2+∠A3+∠A4+∠A5= 度.从上述结论中你发现了什么规律?
如图5,MA1∥NAn , 则∠A1+∠A2+∠A3+…+∠An= 度.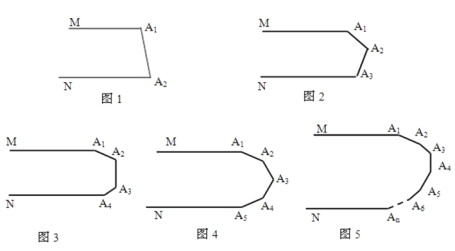
-
科目: 来源: 题型:
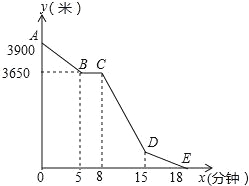
查看答案和解析>>【题目】小丽的家和学校在一条笔直的马路旁,某天小丽沿着这条马路上学,先从家步行到公交站台甲,再乘车到公交站如乙下车,最后步行到学校(在整个过程中小丽步行的速度不变).图中折线ABCDE表示小丽和学校之间的距离y(米)与她离家时间x(分钟)之间的函数关系.
(1)小丽步行的速度为 ;
(2)写出y与x之间的函数关系式: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式6a3﹣54a分解因式的结果为__.
相关试题

