【题目】菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
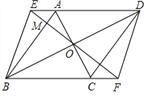
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,tan∠MBO=![]() ,求EM:MF的值.
,求EM:MF的值.
参考答案:
【答案】(1)证明见解析;
(2)EM:MF=1:4.
【解析】(1)证明:在菱形ABCD中,AD∥BC,OA=OC,OB=OD,
∴∠AEO=∠CFO,
在△AEO和△CFO中,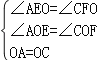 ,∴△AEO≌△CFO(AAS),
,∴△AEO≌△CFO(AAS),
∴OE=OF,又∵OB=OD,
∴四边形BFDE是平行四边形;(5分)
(2)解:设OM=x,∵EF⊥AB,tan∠MBO=![]() ,
,
∴BM=2x,又∵AC⊥BD,∴△AOM∽△OBM,∴![]() =
=![]() ,
,
∴AM=![]() =
=![]() x,∵AD∥BC,∴△AEM∽△BFM,
x,∵AD∥BC,∴△AEM∽△BFM,
∴EM:MF=AM:BM=![]() x:2x=1:4.(10分)
x:2x=1:4.(10分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=
 计算.
计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=
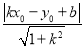 =
=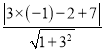 =
=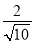 =
=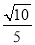 .
.根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=
 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+4x+5(﹣3≤x≤0)的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB∥CD,CE平分∠ACD交AB于E点.

(1)求证:△ACE是等腰三角形;
(2)若AC=13cm,CE=24cm,求△ACE的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(﹣14)﹣(+15);
(2)﹣3﹣4+19﹣11+2;
(3)(﹣4)﹣(﹣1)+(﹣6)+2;
(4)6÷(-2)+(+3)×
 ;
;(5)
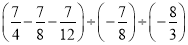 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的方格地面上,标有编号A、B、C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.

(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列长度的三条线段能组成钝角三角形的是( )
A.3,4,4
B.3,4,5
C.3,4,6
D.3,4,7
相关试题

