【题目】如图,AB∥CD,CE平分∠ACD交AB于E点. 
(1)求证:△ACE是等腰三角形;
(2)若AC=13cm,CE=24cm,求△ACE的面积.
参考答案:
【答案】
(1)证明:如图,∵AB∥CD,
∴∠AEC=∠DCE,
又∵CE平分∠ACD,
∴∠ACE=∠DCE,
∴∠AEC=∠ACE,
∴△ACE为等腰三角形
(2)过A作AG⊥CE,垂足为G;
∵AC=AE,
∴CG=EG= ![]() CE=12(cm);
CE=12(cm);
∵AC=13(cm),
由勾股定理得,AG=5(cm);
∴S△ACE= ![]() ×24×5=60(cm2).
×24×5=60(cm2).

【解析】(1)如图,证明∠AEC=∠ACE,即可解决问题.(2)如图,作辅助线;求出AG的长度,运用三角形的面积公式,即可解决问题.
【考点精析】解答此题的关键在于理解平行线的性质的相关知识,掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用科学记数法表示:-0.0000419= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:已知点P(x0,y0)和直线y=kx+b,则点P到直线y=kx+b的距离,可用公式d=
 计算.
计算.例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=
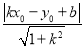 =
=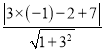 =
=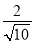 =
=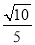 .
.根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=
 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=x2+4x+5(﹣3≤x≤0)的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,对角线AC、BD相交于点O,过点O作一条直线分别交DA、BC的延长线于点E、F,连接BE、DF.
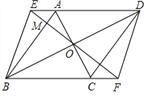
(1)求证:四边形BFDE是平行四边形;
(2)若EF⊥AB,垂足为M,tan∠MBO=
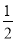 ,求EM:MF的值.
,求EM:MF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算题:
(1)(﹣14)﹣(+15);
(2)﹣3﹣4+19﹣11+2;
(3)(﹣4)﹣(﹣1)+(﹣6)+2;
(4)6÷(-2)+(+3)×
 ;
;(5)
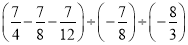 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图的方格地面上,标有编号A、B、C的3个小方格地面是空地,另外6个小方格地面是草坪,除此以外小方格地面完全相同.

(1)一只自由飞行的鸟,将随意地落在图中的方格地面上,问小鸟落在草坪上的概率是多少?
(2)现从3个小方格空地中任意选取2个种植草坪,则刚好选取A和B的2个小方格空地种植草坪的概率是多少(用树形图或列表法求解)?
相关试题

