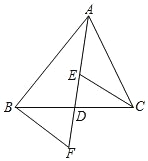
【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE,下列说法:①△ABD 和△ACD面积相等;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE.其中正确的是( )
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
参考答案:
【答案】C
【解析】
根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.
∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,
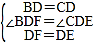 ,
,
∴△BDF≌△CDE(SAS),故③正确;
∴∠F=∠DEC,
∴BF∥CE,故④正确;
∵△BDF≌△CDE,
∴CE=BF,故⑤错误,
正确的结论为:①③④,
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“如果二次函数
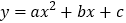 的图象与
的图象与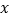 轴有两个公共点,那么一元二次方程
轴有两个公共点,那么一元二次方程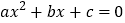 有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若
有两个不相等的实数根.”请根据你对这句话的理解,解决下面问题:若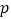 、
、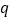 (
(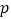 <
<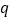 )是关于
)是关于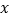 的方程
的方程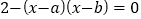 的两根且
的两根且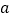 <
<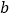 则请用“<”来表示
则请用“<”来表示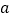 、
、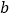 、
、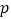 、
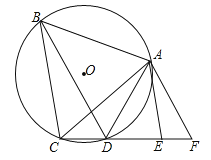
、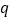 的大小是_________.
的大小是_________. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,∠D=∠C,添加下列哪个条件后,仍不能使△ADO≌△BCO的是( )

A. AD=BC B. AC=BD C. OD=OC D. ∠ABD=∠BAC
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣2(m+1)x+m2+2=0.
(1)若方程总有两个实数根,求m的取值范围;
(2)若方程有一个实数根为1,求m的值和另一个根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O是等边三角形ABC的外接圆,点D在圆上,在CD的延长线上有一点F,使DF=DA,AE∥BC交CF于E.
(1)求证:EA是⊙O的切线;
(2)求证:BD=CF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元),设每件商品的售价上涨
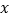 元(
元(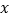 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为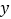 元.
元.(1)求
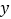 与
与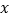 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量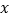 的取值范围;
的取值范围;(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2 200元?
相关试题

