【题目】已知点E,F分别在正方形ABCD的边BC,CD上.若AF平分∠DFE,∠AFE=55°,则∠AEB的度数为( )
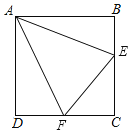
A.75°B.55°C.80°D.45°
参考答案:
【答案】C
【解析】
作AM⊥EF,由题意可证Rt△ABE≌Rt△AEM,可得∠AEB=∠AEF,根据五边形内角和为540°,可求∠BEF=160°,即可求∠AEB的度数.
解:如图:作AM⊥EF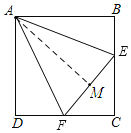
∵四边形ABCD是正方形
∴AB=AD,∠D=∠C=∠B=90°=∠DAB
∵AF平分∠DFE,AD⊥DC,AM⊥EF
∴AD=AM
∵AD=AM,AE=AE
∴Rt△ABE≌Rt△AEM
∴∠AEB=∠AEF
∵∠AFE=55°
∴∠DFE=110°
∵∠B+∠D+∠DAB+∠DFE+∠BEF=540°,
∴∠BEF=160°
∴∠AEB=80°
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
-
科目: 来源: 题型:
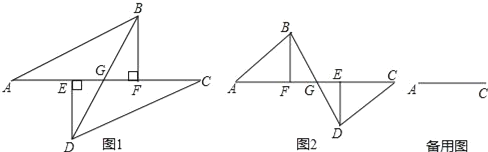
查看答案和解析>>【题目】如图1所示,点E、F在线段AC上,过E,F分别作DE⊥AC,BF⊥AC,垂足分别为点E,F;DE,BF分别在线段AC的两侧,且AE=CF,AB=CD,BD与AC相交于点G.
(1)求证:EG=GF;
(2)若点E在F的右边,如图2时,其余条件不变,上述结论是否成立?请说明理由.
(3)若点E、F分别在线段CA的延长线与反向延长线上,其余条件不变,(1)中结论是否成立?(要求:在备用图中画出图形,直接判断,不必说明理由)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根.
(1)求m的取值范围;
(2)m为何值时,方程有两个相等的实数根?并求出这两个实数根.
-
科目: 来源: 题型:
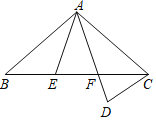
查看答案和解析>>【题目】如图,△ABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
(1)求证:△ABE≌△ACF;
(2)若∠BAE=30°,则∠ADC= °.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,再填空解题:
①方程x2﹣x﹣6=0的根是x1=3,x2=﹣2,则x1+x2=1,x1x2=﹣6;
②方程2x2﹣7x+3=0的根是x1=
 ,x2=3,则x1+x2=
,x2=3,则x1+x2= ,x1x2=
,x1x2= .
.根据以上①②你能否猜出:
如果关于x的一元二次方程ax2+bx+c=0(a≠0,且a、b、c为常数,b2﹣4ac≥0)有两根x1、x2,那么x1+x2、x1x2与系数a、b、c有什么关系?请写出你的猜想并说明理由.
利用公式法求出方程的根即可.
相关试题

