【题目】已知关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根.
(1)求m的取值范围;
(2)m为何值时,方程有两个相等的实数根?并求出这两个实数根.
参考答案:
【答案】(1) 当m≥﹣![]() 时,方程(m+1)x2+2mx+(m﹣3)=0有实数根;(2) m=﹣
时,方程(m+1)x2+2mx+(m﹣3)=0有实数根;(2) m=﹣![]() , x1=x2=﹣3
, x1=x2=﹣3
【解析】
(1)根据题意,分原方程是一元一次方程和一元二次方程两种情况分析讨论即可;
(2)由题意可知,此时原方程是一元二次方程,根据一元二次方程根的判别式求出m的值,并将所得的m的值代入原方程,再解所得方程即可.
(1)关于x的方程(m+1)x2+2mx+(m﹣3)=0有实数根,分两种情况讨论如下:
①当m+1=0即m=﹣1时,原方程是一元一次方程,此时方程为﹣2x﹣4=0,必有实数根;
②当m+1≠0时,此时原方程是一元二次方程,
∵此时原方程有实数根,
∴△=b2﹣4ac=(2m)2﹣4×(m+1)×(m﹣3)=8m+12≥0,解得:m≥﹣![]() 且m≠﹣1;
且m≠﹣1;
综上可知,当m≥﹣![]() 时,方程(m+1)x2+2mx+(m﹣3)=0有实数根;
时,方程(m+1)x2+2mx+(m﹣3)=0有实数根;
(2)∵关于x的方程(m﹣1)x2+(2m﹣1)x+m﹣2=0有两个相等的实数根,
∴△=b2﹣4ac=(2m)2﹣4×(m+1)×(m﹣3)=8m+12=0,
解得:m=﹣![]() ,
,
将m=﹣![]() 代入原方程可得:
代入原方程可得:
﹣![]() x2﹣3x﹣
x2﹣3x﹣![]() =0,
=0,
两边同时乘以﹣2得:x2+6x+9=0,解得x1=x2=﹣3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校举行数学竞赛,需购买
 两种奖品共160件,其中
两种奖品共160件,其中 种奖品的单价为12元,
种奖品的单价为12元, 种奖品的单价为8元,且购买
种奖品的单价为8元,且购买 种奖品的数量不大于
种奖品的数量不大于 种奖品数量的3倍,假设购买
种奖品数量的3倍,假设购买 种奖品的数量为
种奖品的数量为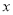 件.
件.(1)根据题意填空:
购买
 种奖品的费用为___(元);
种奖品的费用为___(元);购买
 种奖品的费用为___(元);
种奖品的费用为___(元);(2)若购买两种奖品所需的总费用为
 元,试求
元,试求 与
与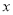 的函数关系式,并求出
的函数关系式,并求出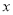 的取值范围;
的取值范围;(3)问
 两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
两种奖品各购买多少件时所需的总费用最少,并求出最少费用. -
科目: 来源: 题型:
查看答案和解析>>【题目】今年5月14日川航3U863航班挡风玻璃在高空爆裂,机组临危不乱,果断应对.正确处置,顺利返航,避免了一场灾难的发生,下面表格是成都当日海拔高度h(千米)与相应高度处汽温t(℃)的关系(成都地处四川盆地,海拔高度较低,为方便计算,在此题中近似为0米).
海拔高度h(千米)
0
1
2
3
4
5
…
气温t(℃)
20
14
8
2
-4
-1
…
根据上表,回答以下问题:
(1)由上表可知海拔5千米的上空气温约为______℃;
(2)由表格中的规律请写出当日气温t与海拔高度h的关系式为______.
如图是当日飞机下降过程中海拔高度与玻璃爆裂后立即返回地面所用的时间关系图.根据图象回答以下问题:
(3)挡风玻璃在高空爆裂时飞机所处的高度为______千米,返回地面用了______分钟;
(4)飞机在2千米高空水平面上大约盘旋了______分钟;
(5)挡风玻璃在高空爆裂时,当时飞机所处高空的气温为______℃,由此可见机长在高空经历了多大的艰险.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,将三角尺的直角顶点P落在∠AOB的平分线OC的任意一点上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F。证明:PE=PF。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等边三角形,D为BC边上一个动点(D与B、C均不重合),AD=AE,∠DAE=60°,连接CE.
(1)求证:△ABD≌△ACE;
(2)求证:CE平分∠ACF;
(3)若AB=2,当四边形ADCE的周长取最小值时,求BD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x+m﹣2=0有两个实数根,m为正整数,且该方程的根都是整数,则符合条件的所有正整数m的和为( )
A. 6 B. 5 C. 4 D. 3
相关试题

